题目链接:http://bestcoder.hdu.edu.cn/contests/contest_showproblem.php?pid=1002&cid=530
(格式有一点点问题,直接粘下来吧)

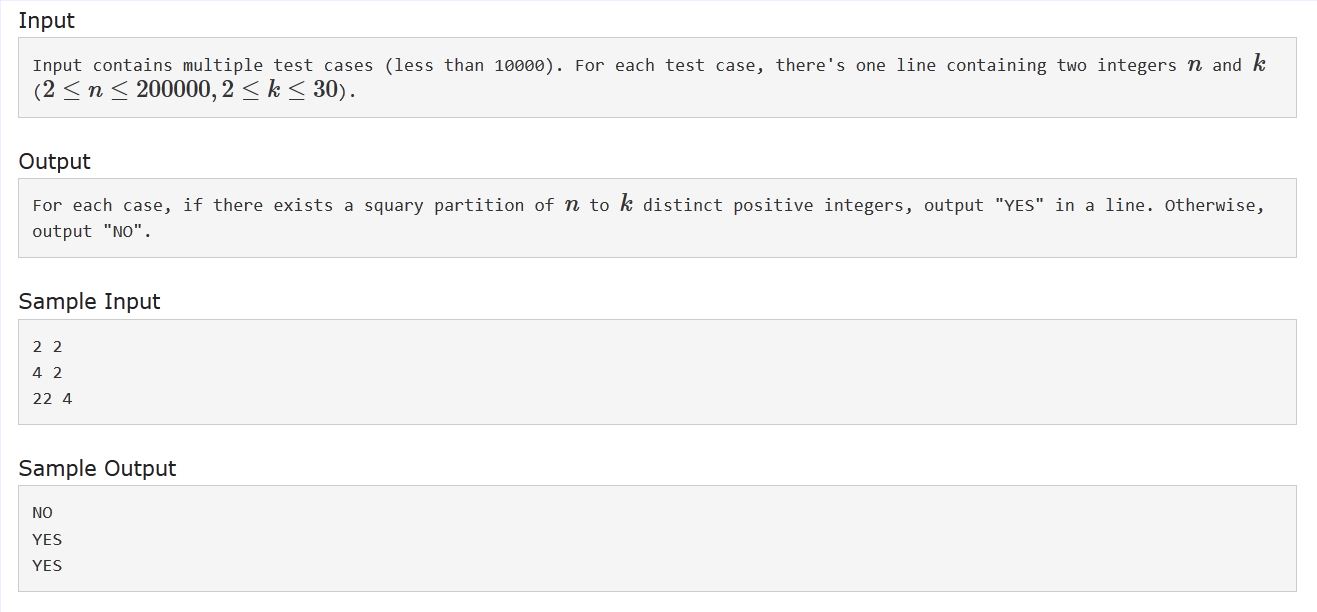
题目意思:给出 n 和 k,问能否构造 k-1个不同的数使得这 k-1 个数(每个数都为正整数)的和等于一个数的平方,且 k 个数(都为正整数)的和等于 n。
错了差不多十多次,终于要看别人思路了.......
为了将问题简化,且保证 k-1 个数都是不同的,我们从自然数1,2,...,k-2 构造出前 k-2 个数,看清楚,不是 k-1 而是 k-2。因为最后第 k-1 个数有待斟酌!!!
设 square 为 k-1 个数之和,也就是等于的某个数的平方啦,remain 就是 n - square了。
先排除两种特殊情况:
(1) remain = 0 (不符合正整数的要求)或者 (k-1) * k /2 > square(因为是从1开始构造的,最小的square 都需要大于等于 (k-1)* k /2(1+2+3+...+k-1) ,避免无谓的计算
(2)如果square = 1 并且 remain = 1 ,那么无解。这就是Sample 中的2 2了。
然后开始构造k-2个数。构造的时候,如果遇到remain(假如为x),就跳过一位,变成x+1,使得构造的数中不包含remain。因此代码中就有 x 多自增1次的操作了。
构造完 k-2 个数之后(设和为sum),我们要对最后一个数,即第 k-1个数进行讨论(代码中的need,它的值等于 n - sum - remain)。如果这个 need <= x (第 k-2 个数的值就是x),代表 k - 1个数中有两个数是相同的,与题意不符。而且它就算怎样调整都不能构造出答案,因为我们是从最小的自然数1开始构造的!
比较难理解的是,最后的那个k-1的数,我们还是x++,但是sum + x 有可能并不等于 (确切来讲是小于,如果是大于都是无解的,从最小数开始构造嘛)square,但是我们可以调整 k-2个数中的某个数ai令它大点--->ai+k,使得sum + x(此时的x不是原来单纯的 x++ 了,x = square-(sum-ai+ai+k)) 不过这些情况比较复杂,所以我们反其道而行之,讨论无解的情况!
无解的时候,有两种情况。最后 前面不是说 x++ 吗,那么第一种肯定无解的情况:x == remain && need == remain!这个表示remain 在k-2个数的构造中根本没有遇到。而且need这个值 是必须的,无论前面怎样调整,还是那个道理,从最小数1开始构造。
最难理解的是第二种情况 x+1 == remain && need == remain (我也想了好久才想通,wa了这么多次就是这个没想出来)。remain 是动不了的,只能从need 和 前面已经构造了的 k-2个数中开刀。
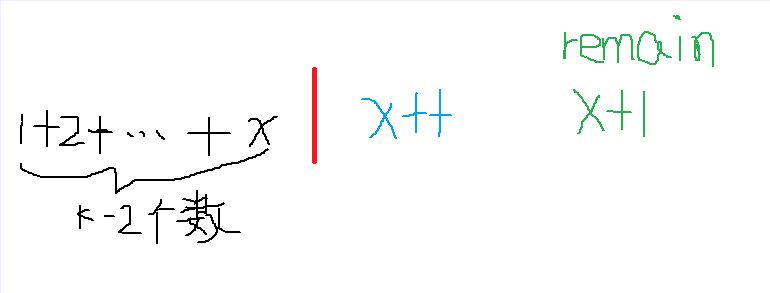
我们不希望need = remain,于是只能让k-2个数中的某个数增加1(确切来讲只能是黑色字体的x,因为数与数之间是紧挨着的),变成蓝色部分的x++,此时need 确实不等于 remain,但是need 却等于蓝色部分的x++(need - 1)了,也就是最后构造出来的k-1 个数中有两个数是相同的!!!
只要排除这两种情况,就表示可以得出解。

1 #include <iostream> 2 #include <cstdio> 3 #include <cstdlib> 4 #include <cstring> 5 using namespace std; 6 7 int n, k; 8 9 bool check(int square, int remain) 10 { 11 if (remain == 1 && square == 1) // k = 2, remain = 1的情况 12 return false; 13 int sum = 0; 14 int x = 0; 15 for (int i = 0; i < k-2; i++) // 构造k-2个数 16 { 17 x++; 18 if (x == remain) 19 x++; 20 sum += x; 21 } 22 int need = n-sum-remain; 23 if (need <= x) // 最后第k-1个数在前k-2个已构造数里面 24 return false; 25 // need > x(未自增前),有可能与remain有冲突(remain在k-2个数之外) 26 x++; 27 if (x == remain || x + 1 == remain) 28 { 29 if (need == remain) // need == remain == x 30 return false; // or need == remain == x+1 31 } 32 return true; // need > x+1 33 } 34 35 int main() 36 { 37 while (scanf("%d%d", &n, &k) != EOF) 38 { 39 int flag = 0; 40 for (int i = 1; i * i < n && !flag; i++) 41 { 42 int square = i*i; 43 int remain = n - square; 44 if (remain == 0 || (k-1)*k/2 > square) 45 continue; 46 if (check(square, remain)) 47 { 48 flag = 1; 49 break; 50 } 51 } 52 printf("%s ", flag ? "YES" : "NO"); 53 } 54 return 0; 55 }
