LeetCode-846.一手顺子
题目链接(微信打开):https://mp.weixin.qq.com/s/RWzrpg1Q4Dke7UNR4T34PA
一、题目描述
Alice有一手牌:整数数组hand,需要将它分组,问是否可以将其分成每组牌数都是groupSize张,且每组牌数的数字需要连续。可以的话输出:true,否则:false。
示例 1:
输入:hand = [1,2,3,6,2,3,4,7,8], groupSize = 3
输出:true
解释:Alice 手中的牌可以被重新排列为 [1,2,3],[2,3,4],[6,7,8]。
示例 2:
输入:hand = [1,2,3,4,5], groupSize = 4
输出:false
解释:Alice 手中的牌无法被重新排列成几个大小为 4 的组。
注意:
-
1 <= hand.length <= 104
-
0 <= hand[i] <= 109
-
1 <= groupSize <= hand.length
二、题目分析
先说说自己能想到的和不能想到的一些问题吧~~~
(I)能想到的
这个hand数组能不能分成每组为:groupSize个数,首要条件需要满足:
1、hand的个数能被groupSize 除尽,即:
hand.length mod groupSize == 0
2、需要对整个hand数组,进行从小到大的排序
3、要统计每个数字的出现次数
用另一个数组cnt,cnt[hand[i]] 表示hand[i] 这个数的出现次数。比如,未对数组hand排序前,hand[2],hand[7],hand[11],hand[18]都是数字3,那么cnt[3]=4。
4、当某个hand[i]能分成一对顺子后,这个hand[i]要被剔除,然后出现次数要递减1。
拿上面的示例2来说,没成顺子前应得到次数数组:
cnt[1]= 1 cnt[2]= 2 cnt[3]= 2 cnt[4]= 1 cnt[6]= 1 cnt[7]= 1 cnt[8]= 1
当把1,2,3成一对顺子后,次数数组变成:
cnt[1]= 0 #成顺子,次数减去1 cnt[2]= 1 #成顺子,次数减去1 cnt[3]= 1 #成顺子,次数减去1 cnt[4]= 1 cnt[6]= 1 cnt[7]= 1 cnt[8]= 1
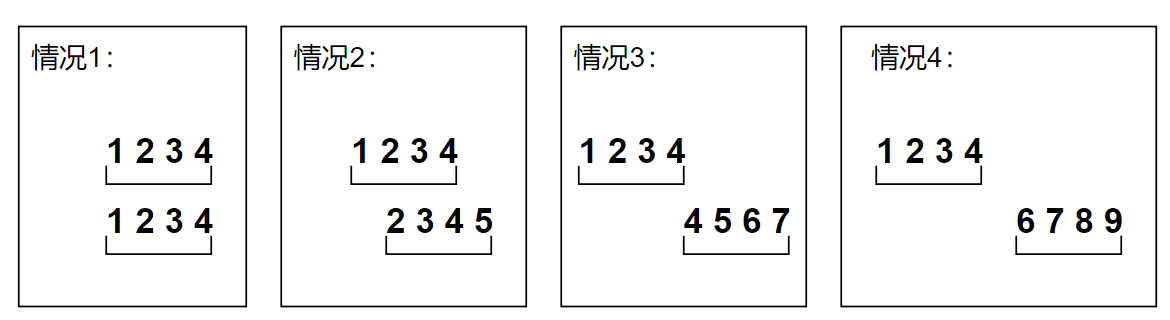
5、最后就是成顺子的一些组合,数字有重叠的是情况1~3,数字不重叠的是情况4
(II)不能想到的
上面都是些零碎的分析,如何窜代码,成了我一道坎。
主要体现在:
(1)当从hand数组拿走一对groupSize牌数后,次数数组相应的递减1,之后如何保证hand数组,最终剩下的牌能不能刚好都成顺子;
(2)这个位置移动怎么移动,例如上面图的情况1,需要分成每组groupSize=2的顺子,当从中拿走1、2成顺子后,下一个顺子位置是从3、4,还是从1、2去拿,如果从3,4去做顺子,怎么折返回去拿1,2。然后就被自己搞混了。
三、最终解析
后来我看了题解,发现没想象中复杂!以下摘自题解:
假设尚未分组的牌中,最小的数字是 x,则如果存在符合要求的分组方式,x 一定是某个组中的最小数字(否则 x 不属于任何一个组,不符合每张牌都必须被分到某个组),该组的数字范围是 [x,x+groupSize−1]。
再将 x 到 x+groupSize−1 的 groupSize 张牌分成一个组之后,继续使用贪心的策略对剩下的牌分组,直到所有的牌分组结束或者无法完成分组。
如果在分组过程中发现从最小数字开始的连续 groupSize 个数字中有不存在的数字,则无法完成分组
对第一个疑问,其实是我顾虑太多了。首先,hand数组能被groupSize除得尽,如果都能成顺子配对的话,是不会存在多余的数成不了顺子的。
第二个疑问:怎么移动下一对顺子的位置。排完序依次顺着来,直到次数数组递减到0,我们再移动位置就好了。
刚前面提到情况1的图,如果1、2成顺子,下一个顺子位置应从1、2去组顺子,而不是直接拿3,4去组。 因为cnt[1]和cnt[2]还没成0。
假设n表示hand数组的长度,伪代码如下:
#1、声明一个次数数组 cnt[1~n] = 0 #2、输入hand[1~n]的同时,统计每个整数出现的次数,注意,有可能某些cnt[x]会为0 cnt[hand[i]] ++ #i的取值为:1~n #3、对hand[1~n]从小到大排序 sort(hand, hand+n) #4、判断是否能被n除尽,不能则表示分不了每组为groupSize的顺子,返回False if (n mod groupSize != 0) return False #5、遍历hand,是否能恰好分组:每组都为顺子 ##表示下一次移动的位置 for (i=1; i <= n; i++) #刚好次数被递减到0,或者cnt本来就为0,跳到下一个需要比较的位置 if (cnt[hand[i]] == 0) continue ##表示顺子的取数,是相对hand[i]去取的 for j in range(hand[i], hand[i]+groupSize-1) #如果组不了顺子,返回False if (cnt[j] == 0) return False #能组成顺子,次数减去1 cnt[j]--
#全部数字,确认过都能组成顺子
return True
最后,感叹下,python的代码确实写下来比其他代码要短很多~~~
还有,时间复杂度和空间复杂度,大家请参考微信的分析。。。