风螺旋线公切线的算法
在DOC8168所有成型的模板里,都隐藏着这样一个事实,同一个模板里所使用的风螺旋线基础参数是相同的。比如:等待与基线模板中,入航与出航采用的是最高点的高度来考虑风速。转弯半径、偏流角在同一个模板中也都是相同的。本质上说这是为了对计算进行简化,同时又不降低安全裕度而进行的设定。在讨论风螺旋公切线算法时,可以基于这种简化的前提条件来加以分析。
Eθ分量在风螺旋中代表了风速向量的方向,而风螺旋的切线代表了地速向量的方向,二者相垂直时,风螺旋线所包含的范围最大,因此,风螺旋线的切线必然垂直于它自身的某个Eθ分量。
对于公切线来说,如果在两条风螺旋线之间存在有一条公切线,那么这条公切线必然分别垂直于两条风螺旋线中的某个Eθ分量,并且这两个Eθ分量互相平行。
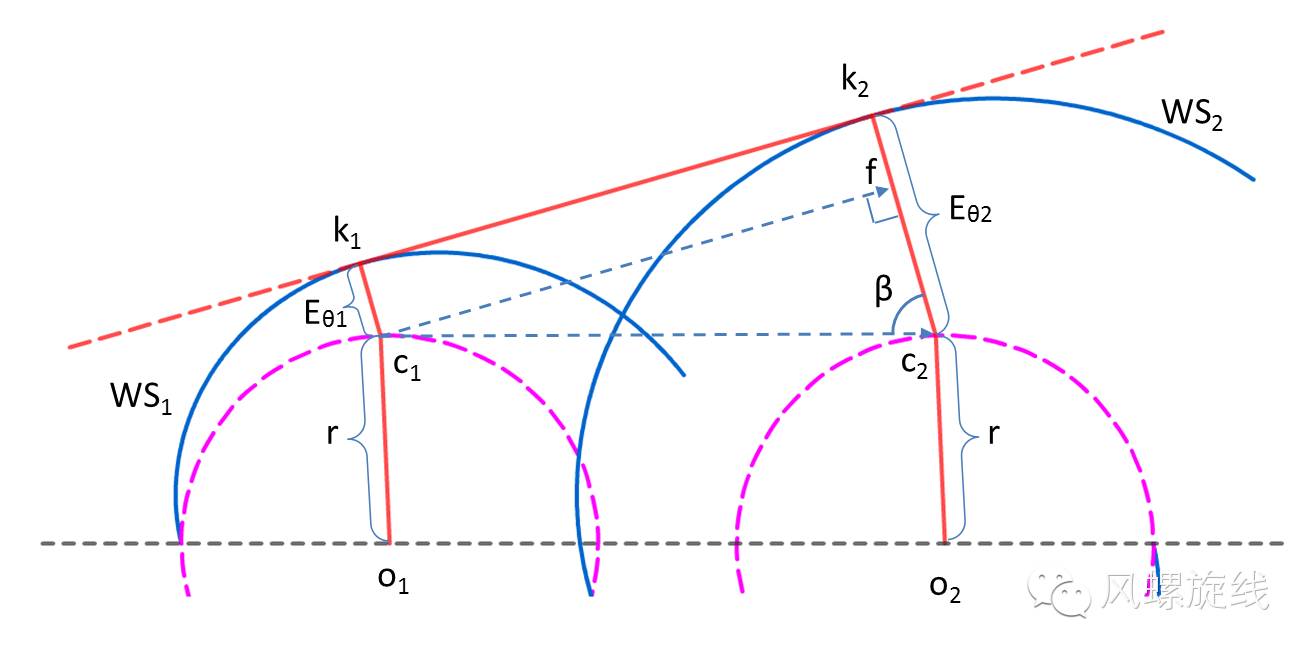
上图中标绘了两条初始角度相差180°的风螺旋线(WS1与WS2),以及它们之间的公切线(k1k2)的位置关系。除了初始的角度不同外,两条风螺旋线采用了相同的基础参数,因此,它们具有相同的转弯半径与偏流角。
根据前述的分析,Eθ1与Eθ2同时垂直于k1k2线,由于Eθ1与对应半径r的延长线的夹角始终是DA(偏流角),因此可知,线段o1c1与线段o2c2相互平行,由于两条风螺旋线的基准半径r相同,故o1o2c2c1是一个平行四边形,线段c1c2的长度等于线段o1o2的长度。从c1点向c2k2作垂线,得到f点,线段c2f的长度就等于Eθ2减去Eθ1的长度。
在系统中添加两条风螺旋线时,它们的基准圆心点的距离是已知条件,二者初始角度的差值也是已知条件(如果某个风螺旋线初始时带有外扩距离,可将初始外扩的距离换算成角度累计起来),因此,在直角三角形fc1c2中可以计算出β的角度值。
公切线所对应的Eθ1与Eθ2长度的差别可以看作是两条风旋转线初始角度的差异所造成的。线段fk2与Eθ1长度相等,可以看作是两条风螺旋共同旋转过的角度(根据之前的分析,相同的参数旋转相同的角度,会得到相同的外扩距离)。
β=arccos((Eθ2-Eθ1)/o1o2)
β角是基于圆心点的连线o1o2计算得到的,在此基础上,只需要分别计算出风螺旋线初始角度与圆心连线角度之差,累加上DA之后可以分别得到计算切点所需的θ角。
本例中:WS1初始角度与圆心连线的夹角为零,切点k1对应的θ1 =β+DA。WS2初始角度与圆心连线的夹角为180度,故θ2 =180+β+DA。
实际中的效果图(θ1与θ2取不同的值)可以是如下图中的样子,图中未隐藏掉公切线以内的部分,看外围曲线就行了。

当Eθ1大于Eθ2时,β角是钝角,相关算法仍然成立。情况如下图所示:

当Eθ1等于Eθ2时,这种情况在转弯大于75°的离场、复飞中最为常见,此时,β角等于90度,切点对应的θ角等于90°+DA。(欢迎验证)
由于主区、副区可以共用同一个θ角(参考风螺旋线外扩一文),因此,在计算出一个θ角之后,相关的副区边界的切点也就可以计算得到了。

如果两条风螺旋线的标称转弯半径不同,偏流角不同,根据切线原理得到的四边形o1o2c2c1必然不是平行四边形,相关的计算方法需要额外的考虑,这类问题就留给数学精英们去探讨吧。
今天是2015年感恩节,分享一段自己认为是风螺旋线中最核心的算法思路给大家,感谢一直以来各位的关心与帮助,谢谢你们!
如果这里讨论的话题让你有挫折感,完全不必担心,因为这个系列的话题我也是经过近两年的龟速思考才逐渐理清的。难度是有的,但如果对你的工作有帮助,花上一些时间来读一读,一起体会一下领先于规范的感觉,还是蛮有趣的。每每想到今天的话题也许就是未来飞行程序的入门课,心里还真是有些小激动噢。
感谢大家的关注,如果经你的验证,认为这里的理论是正确的,欢迎广泛传播,如果是有错误的请直接给我留言,再次感谢!
更多文章,请在关注“风螺旋线”微信公众号后,通过历史消息查看。
微信扫一扫
关注该公众号