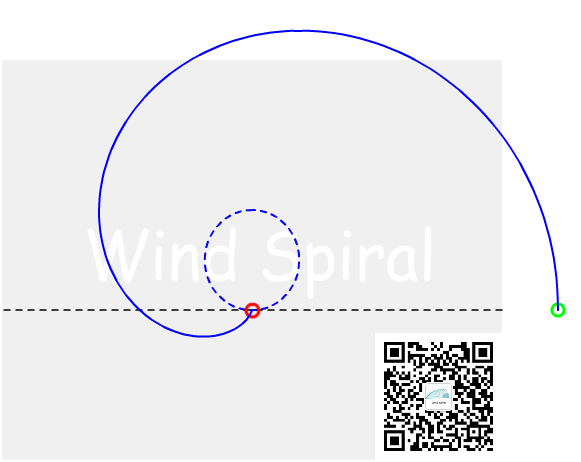
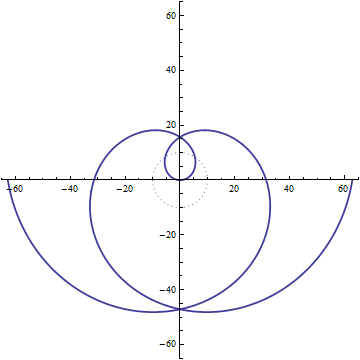
螺旋线可以用直线运动与圆周运动相叠加来产生,在这样旋转的空间里,所有的维度不再是直线式的,而是螺旋式的。
- 所谓的“圆满”只是“止步不前”
我们可以通过数学公式来证明,如果直线运动不存在了(速度为零),螺旋线会变成一个标准的圆。这就像是如果失去了方向,每一天的时光只会变成简单的重复,所以有一个持之以恒的目标对于人生而言是非常的重要。
如果圆周运动不存在了,螺旋会伸展成一条直线,了无挂碍却单调而无趣。这就像是我们的生活终究是需要一些牵绊的,正是这些放不下的牵绊才让我们的轨迹变得如此的丰富和深刻。

2. 螺旋打破了对称,却在更大的范围内找到了对称
螺旋线一直以来,从未给人以对称的感觉,现在看来,这仅仅是因为,我们只看到了它从圆心走出来的那一半轨迹。而它在穿越圆心之前的那一半轨迹从未被认真的解读过。

如果世界真的是从一个点爆发而来,那么世界必定存在一个收缩回一个点的过程,螺旋线似乎就是在平面空间里对这一过程进行的描述。
3. 世界不仅是对称的而且还是互补的
相同的直线运动,在顺时针旋转和逆时针旋转的条件下,会产生两种不同的螺旋,这两种螺旋可以精确的相切与某一个位置点,形成互补的效果。传统文化讲究阴阳,讲究互补,如果用螺旋线来解释,那就是旋转方向的不同造成了这样的结果。

4. 等距螺旋的无差别心
旋转的方向不同,螺旋的外观会有差别,但仅从外观来看,是否可以判断是顺时针旋转还是逆时针旋转呢?答案是无法判断。因为顺时针旋转形成的螺旋,换个位置用逆时针旋转同样可以形成。直线从左向右的运动,可以反过来看成是从右向左的运动。所以螺旋应该看成是运动所留下的轨迹,而不是运动的本身。从运动轨迹的形成来说,顺时针或逆时针、向左还是向右都可能产生相同的结果,所以是没有分别。
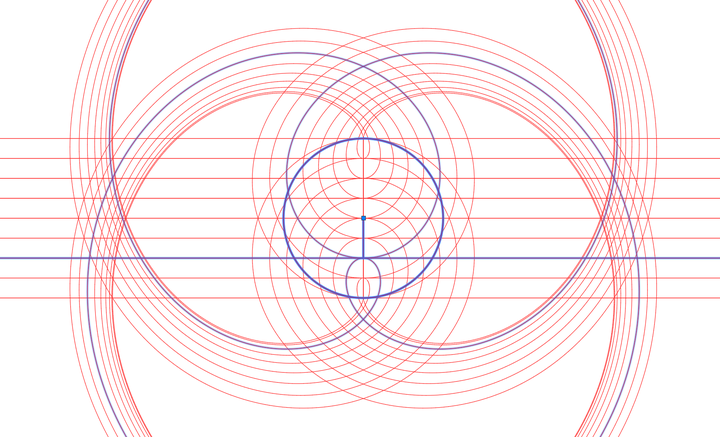
现代物理的“弦理论”,我完全不懂,但隐约感觉它是把运行形式当成了物质构成的成分。所有物质都在运动,受各种引力的做用,呈现出不同的螺旋,但这只是运动形式而已,并不是它实际的元素。
5. 等距螺旋的平等心
如果让直线从圆周的不同位置出发,来绘制螺旋线,每个旋转周期保持相同的跨度。经过多个旋转周期之后会发现,原来分散的螺旋逐渐的变得密集,仿佛越来越趋于相同(螺旋的趋同性)。
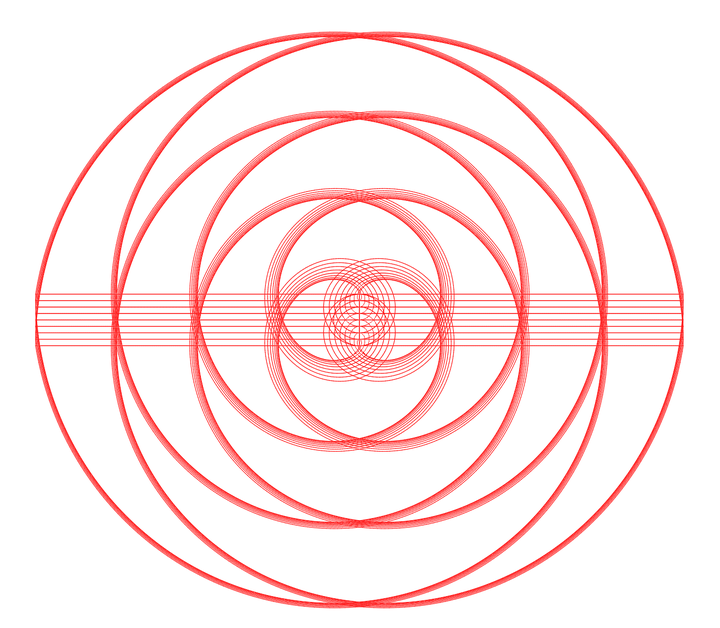
形成这样效果的原因是,初始位置的差异放到更大的范围内来看时,所占的比重会越来越小,因此,基础参数相近的螺旋,最终都会趋于一致。起点高低与最终能走多远,并没有太多直接的关系,最重要的是方向的笃定以及长期的坚持。这和“道无高下之分”非常的契合,方向一致,最终的路径必然会接近。

6. 万千法门皆可得道
如果螺旋是从圆周上的同一个点出发,向着不同的方向去运动,会产生如下图的结果。
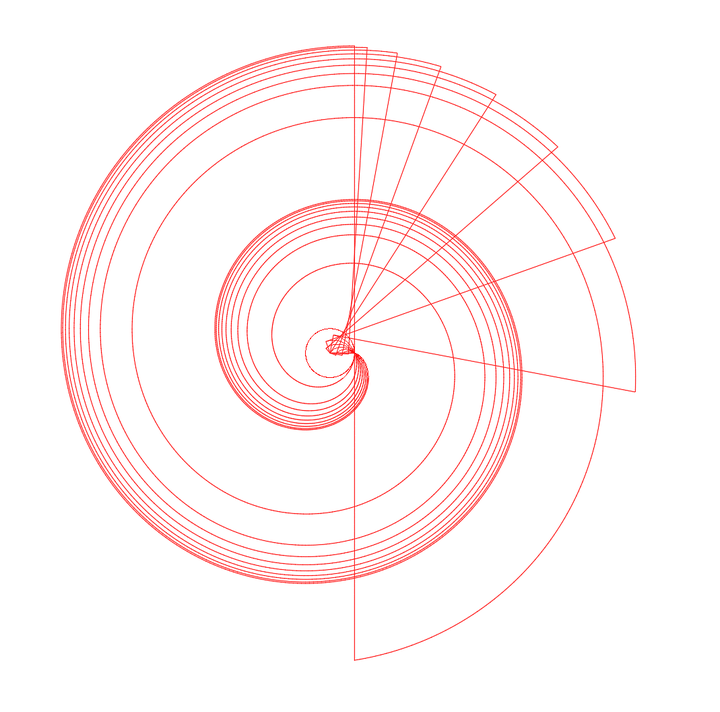
我们再把另一个旋转方向也添加进来,最中心的图形是下面的效果。

这里的直线段是用来描述螺旋外扩的方向,它与螺旋的初始位置点相切。
整体来看螺旋将是下面的效果。
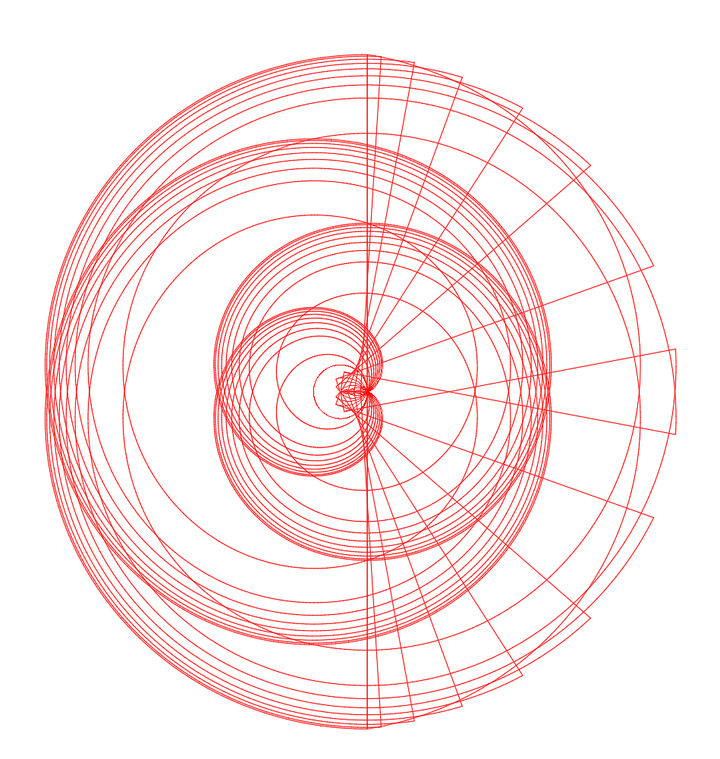
如果把远离圆心的某个地方称为彼岸,那么无论向着哪个方向去运动,或迟或早最终都将到达彼岸。佛教讲究万千法门终可得道,从这个意义上来讲还是说得通的。那么这里的前提条件是走的足够的久远,或是对目标的发散有足够的抵抗力。这就好比,我们知道穿越地心,是地球上两点之间的最短路径,但这条路径上需要克服的困难是普通的生命体所无法企及的(至少目前为止是这样)。
2020即将到来,等距螺旋的普及之路还非常的漫长,愿未来的日子里,等距螺旋和大家一起共同成长,探索未知的边界,走出属于自己独有的那条轨迹!
CAD文件下载见附件。
链接: https://pan.baidu.com/s/1KNmD9kfUheFfnG6KTEJL0Q 提取码: s31s
相关文章链接:
刘崇军:论渐开线的“正确”打开方式