
等距螺旋1周岁生日快乐!
2018年6月,《等距螺旋的原理与计算》正式刊发,到今天正好有一年的时间了,为了有一个更好的仪式感,把6月9号当做是等距螺旋的生日来庆祝一下。
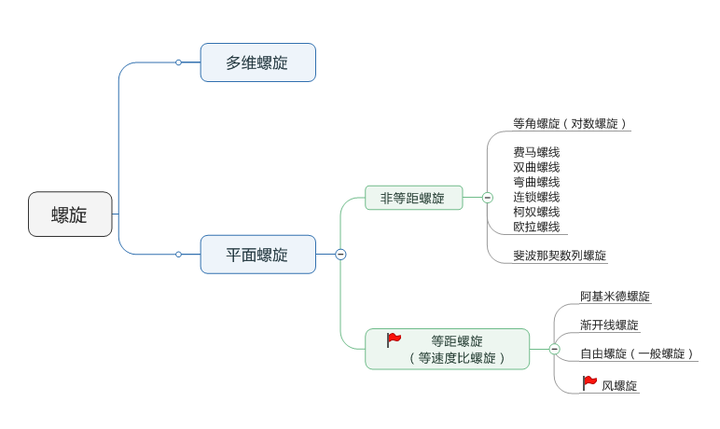
对螺旋了解的越多,就越容易发现我们对世界的认知多么有限。仅从目前的阶段来看,螺旋可以按照下面的框架进行划分,等距螺旋与风螺旋只是这框架中一个小小的角落。
过去我们用匀速直线运动与匀速旋转运动相结合来描述阿基米德螺旋。现在看来,这是不恰当的,阿基米德螺旋可以用下面的公式 来表示:
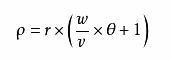
公式中用特定的半径r,圆周上的旋转速度v与直线运动的速度w之比,来表示阿基米德螺旋,角度为弧度单位。从公式中可以看到,当速度成倍增加时,计算结果不会发生变化,也就是说阿基米德螺旋的大小与速度没有直接关系,而与速度之比有关系。
从阿基米德螺旋公式中剥离出一个半径以后,可以想像到直线与圆周必然存在位置上的不同关系,而阿基米德螺旋仅仅是直线穿过圆心的那一种情况。
在传统的螺旋线中,渐开线正是直线与圆周相切的一种情况。渐开线的极坐标系公式可以用下现的形式来表示:

实际上渐开线对于运动形式的要求是很多的,首先,直线运动的速度应与圆周运动的速度相等,其次在圆周相切的位置,直线的运动方向与圆周运动方向相反,只有这样才能形成渐开线螺旋。
直线与圆周相切,可以搭配各种的速度比,因此,这个位置上的螺旋是无限多的,事实上也正是如此,渐开线只是众多与圆周相切的螺旋中最特殊的那一个。
直线与圆周相交,同样可以产生大量的螺旋,在这一类的螺旋中,风螺旋是速度比等于(直线至圆心的)距离D与(圆周)半径r之比的螺旋,风螺旋的公式相对复杂一些,是下面的样子:

风螺旋对运动方向的要求与渐开线相同,渐开线可以看做是DA角为90°的风螺旋(D=r)。风螺旋公式是等距螺旋的通用公式,其余螺旋的公式均可以通过风螺旋公式化简得到。
等距螺旋是真正按照直线运动与圆周运动的叠加来分析螺旋的,现有的绝大多数螺旋实际上只是一半的螺旋,并不是完整的“螺旋曲线”。完整的螺旋曲线有哪些特征呢?
1、完整的等距螺旋是轴对称图形(对称性)。
螺旋运动包含两个部分,从无限远处通过旋转逐渐收缩到直线与圆心的最近点(称为近地点),以及从近地点旋转扩张再走向无限远的部分。这两部分是轴对称的,对称轴就是过近地点,与直线相垂直的那条直径。
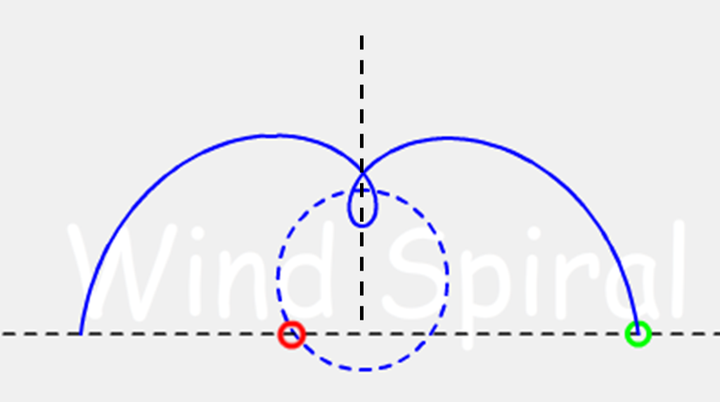
螺旋线并不总是穿过圆心的,正如渐开线展示给我们的情形一样。
2、每一条等距螺旋都有一条与它互补的螺旋(互补性)。
对于同一个直线运动,通过顺时针和逆时针旋转,可以得到两条螺旋曲线,这两种螺旋称为互补螺旋。它们二者在公式上是很大的相似性,是容易引起混淆的概念。
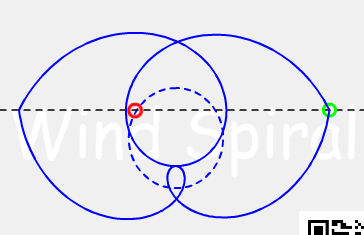
3、等距螺旋在基圆之外的部分总是趋于相同的(趋同性)。
当旋转的周期不断增加之后,因初始位置不同所导致的螺旋之间的差异将逐渐减少。也就是说初始位置的差异在较长周期内所占的比重是逐渐减小的。
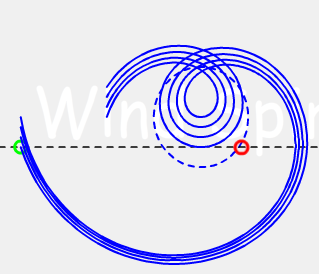
对于等距螺旋来说,各类螺旋最重要的区别主要体现在基圆以内的部分。阿基米德螺旋与风螺旋在基圆以外的部分,有时候非常的近似,这是很多人将二者混淆的一个主要原因。
4、螺旋可以看作是一种运动轨迹,但不能直接用来确定运动的方向(不确定性)。
顺时针旋转所形成的轨迹,可以用逆时针的旋转运动来实现,类似时光倒流的效果。因此,从螺旋曲线本身是无法判断运动的方向。
【等距螺旋概念产生的条件】
1、计算机绘图是等距螺旋产生的基础条件,想要手工精确的绘制一条螺旋线是一件非常困难的事情,只有通过自动化的方法,才可能在大量的绘图之后发现众多螺旋之间的差别与共性。
2、风螺旋是打开等距螺旋之门的那一把钥匙。螺旋的研究并无多少现实的意义,这也是这个学科比较冷门的原因。风螺旋实际上伴随着航空工业的成长已有半个多世纪的历史,只是一直没有实现公式化的描述。当风螺旋的相关问题都解决的时候,等距螺旋的大门也就因此而打开。
【非等距螺旋的联想】
传统螺旋给人们的印象是匀速直线运动与匀角速度运动的叠加,这样的思路无法解释渐开线打开的快慢并不影响它的形状。等距螺旋从公式上很好的解释了这一问题,直线运动的速度与圆周运动的速度之比保持恒定,是形成等距螺旋的前提条件。
如果速度比不能保持恒定,螺旋将出现收缩或扩散的状况。换句话来说,我们所知的各种不按照等距离外扩的螺旋,都可用直线加速度或减速运动与圆周运动的叠加来进行解释。
除了速度比的变化之外,还可以知道的是直线运动不一定过圆心,对于非等距螺旋同样适用(现有的非等距螺旋大多是过圆心的运动形式)。这意味着,我们可以任意使用一套高阶多项式的计算公式叠加到直线运动的表达式上去,从而得到属于自己的特定的螺旋。可以预见的将来,螺旋线的种类将迎来爆发式的增长,对于特定螺旋的命名也将不再是数学家的专利。