若将螺旋看做是直线运动与圆周运动的叠加,每个旋转周期,直线上移动相同的距离,这样得到的螺旋曲线可以统称为等距螺旋。
【等距螺旋的特例】
常用的等距离外扩的螺旋有三类:阿基米德螺旋、渐开线螺旋、风螺旋。
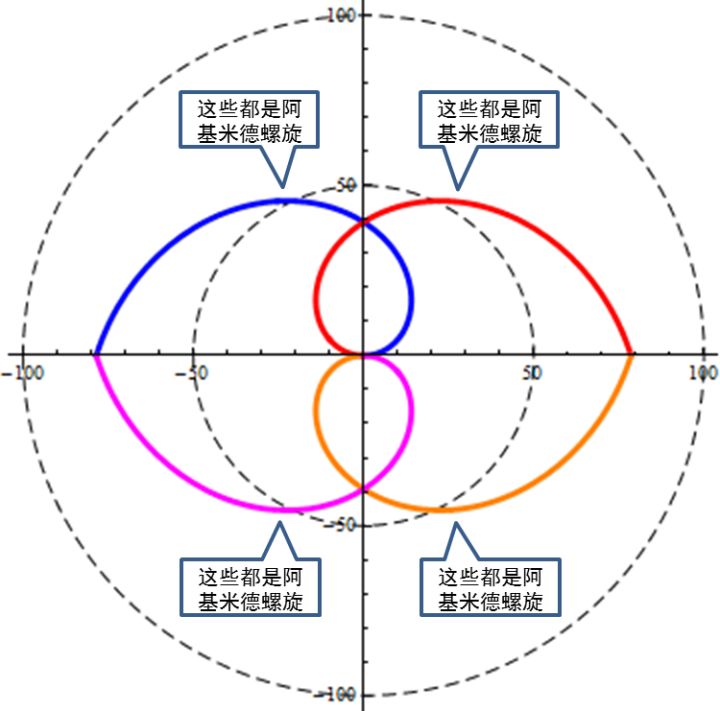
阿基米德螺旋是直线运动穿过圆心时,所形成的螺旋。阿基米德螺旋的互补螺旋仍是阿基米德螺旋。
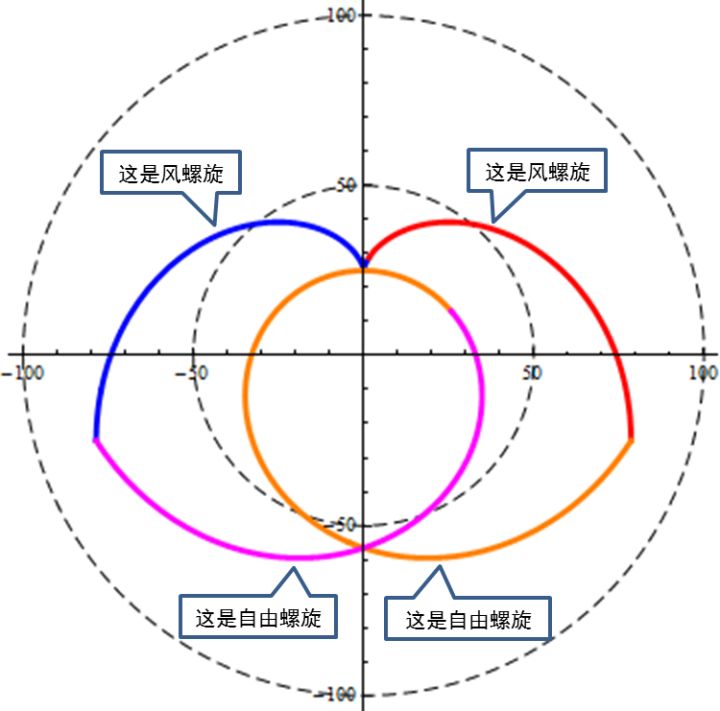
风螺旋是直线与圆相交,并且速度比w/v等于sinDA的情况下出现的一种螺旋,它的互补螺旋不是风螺旋。
渐开线螺旋是直线与圆相切,速度比等于1,在圆周位置点上直线速度与圆周速度方向相反的条件下所产生的螺旋。它的互补螺旋不是渐开线。
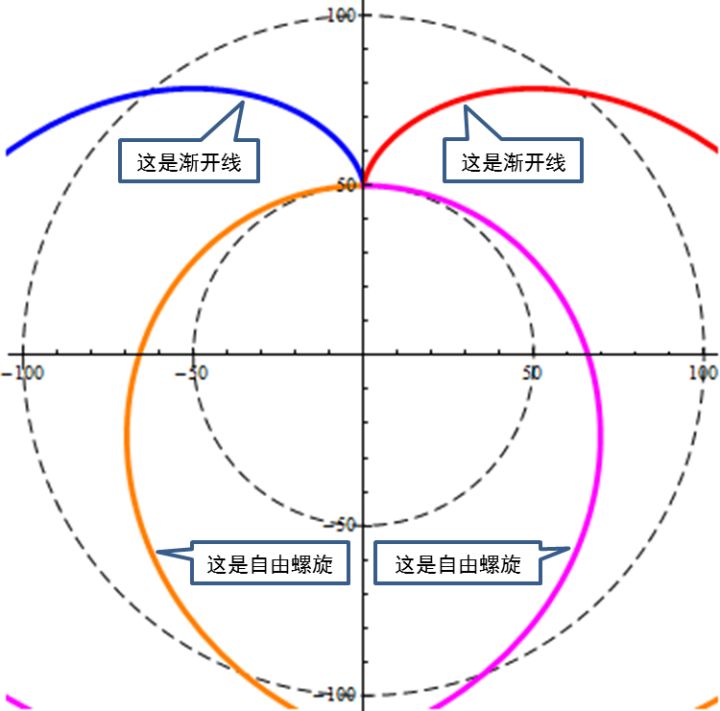
以上三种特例中,阿基米德螺旋数量最多(实际上可理解为无限多),对于特定的半径与直线位置,风螺旋及渐开线都是仅有一条。
除了这些螺旋之外,还有大量的等距螺旋存在,它们的直线运动不过圆心,速度比与位置之间没有特定的要求,它们的切线变化趋势相似但不平行,这些看起来都非常相似,没有特定限制条件的螺旋,可以用一个统一的名字“(等距)自由螺旋”来为它们命名。(网上搜到的另一种名字是:一般螺旋)
【等距螺旋的各种变化】
改变速度比,可以得到不同的自由螺旋。
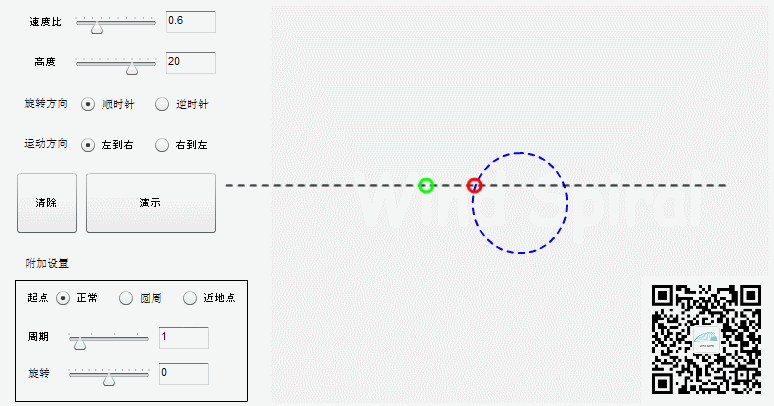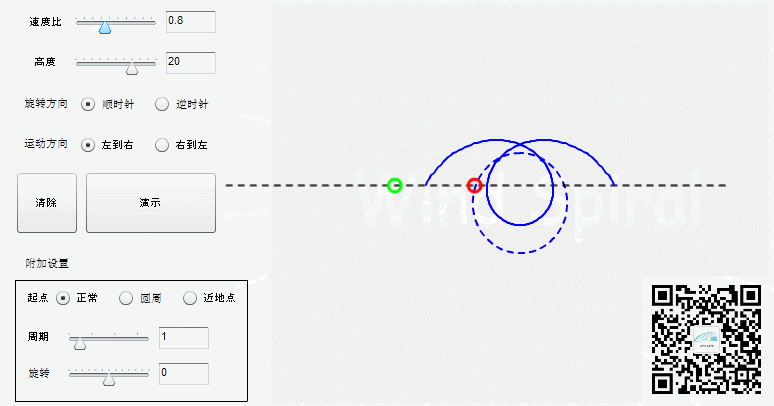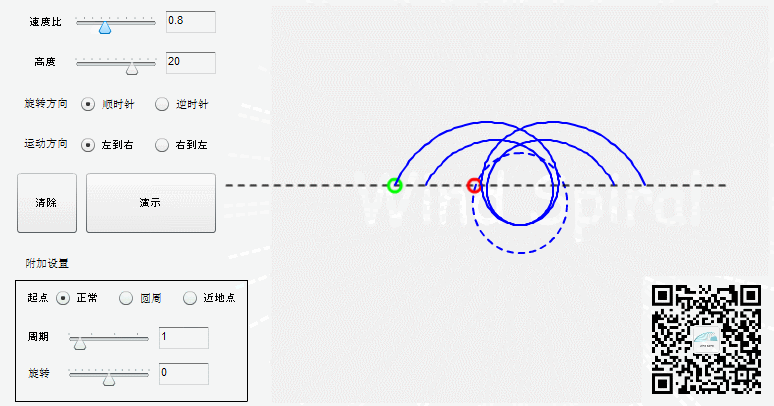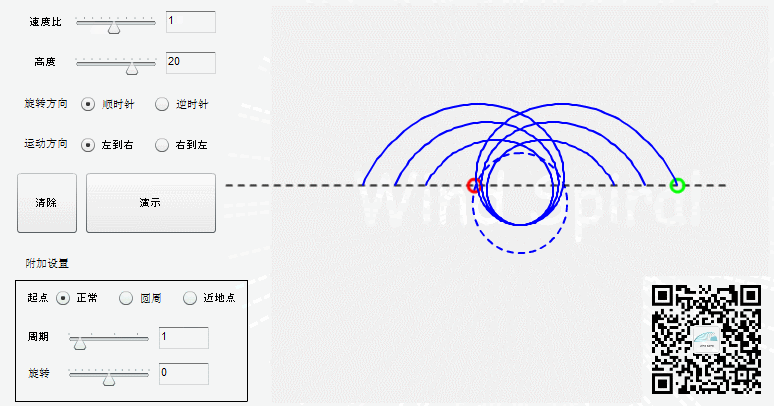
速度比影响每一周期螺旋前进的跨度,基圆半径的大小决定了螺旋变化幅度的大小。
改变直线与基圆的位置关系,也可以得到不同的自由螺旋。

从横向来看,不论直线位置的高低,每个旋转周期水平方向都是外扩了相同的距离。从螺旋与圆周相交的一点来看,风螺旋或是渐开线是外扩效率最高的螺旋。
由上面的图还可以看到,等距螺旋的主要变化都是发生在基圆以内的范围,基圆以外的部分都是相似的。
【w与v的大小变化】
当w<v时,改变DA角,等距螺旋的角度变化规律如下图所示:
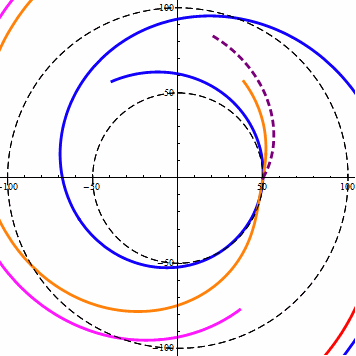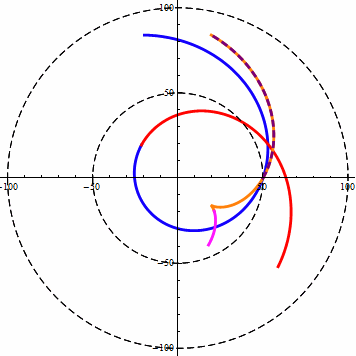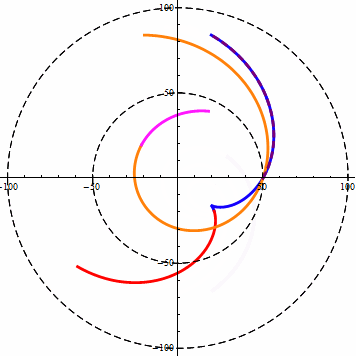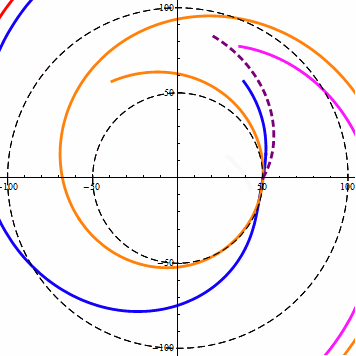
注意第一项限内的虚线螺旋,它是一条风螺旋,当w小于v时,风螺旋的外扩效率是最大的。
当w>v时,改变DA角,等距螺旋的角度变化规律如下图所示:
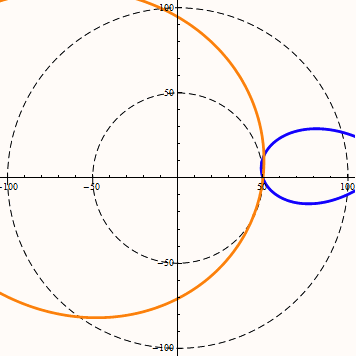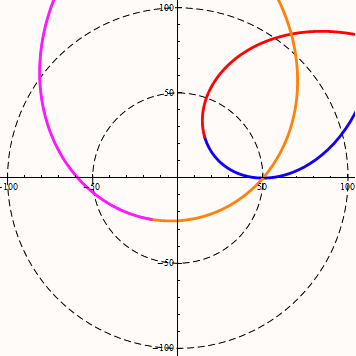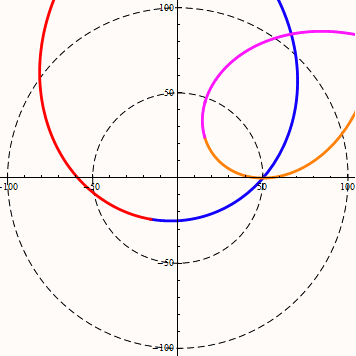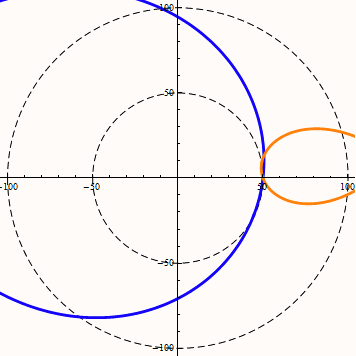
当w大于v时,DA角越接近90度(或-90度)螺旋的外扩效率越高。
在等距螺旋中DA角代表了直线与圆周相交果,交点位置处的半径与直线的夹角。sinDA等于直线距圆心的距离D与半径r的比值。DA的范围为(-90,90)。
【自由螺旋的数量】
从圆心至圆周的半径可以细分成无限多的点,若将这些点当成是螺旋的起点,每一个起点又可以引申出无限多的速度比的组合,因此,自由螺旋的数量是无限多的。
假如“无限多”可以分成几个等级,那么自由螺旋是数量级最大的,其次是阿基米德螺旋,之后是风螺旋,渐开线是数量最少的一种螺旋。
【C螺旋的淡出】
之前根据三角形的关系,发现阿基米德螺旋是v与w相垂直的三角形结构,风螺旋是w与gs相垂直的三角形结构,于是设想v与gs相垂直的三角形结构为C螺旋。
但是根据切线特征来看,C螺旋与阿基米德螺旋的切线变化趋势是近似的,与风螺旋、渐开线在切线上有着显著的区别。
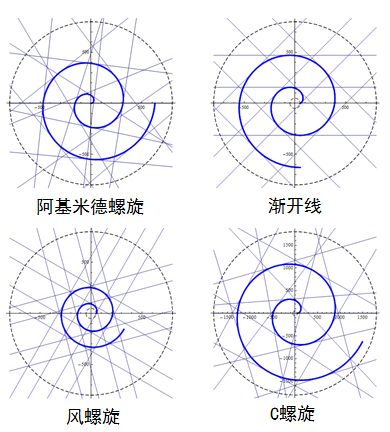
尽管我很希望有一个专属于自己的特例螺旋,但是显然当w大于v时(速度比大于1时),等距螺旋不再考虑外扩效率方面的特性,而C螺旋也只这其中普普通通的一员。
又或者,我们所认为的特例,只是我们眼中的“特例”,放在广袤无垠的时空背景下,所有的特殊都只是特定条件下的一次巧合,我们只是在努力还原大自然的真实意图罢了。
原本想写得更简单明了一些,但还是避免不了的复杂了,权当是记笔记好了,希望能给大家提供一些参考。
(测试软件及代码请参考之前的文章)