Educational Codeforces Round 104 (Rated for Div. 2) A B C D E

比赛链接

A - Arena

有n个英雄，分别由ai的初始等级。每次两个英雄战斗，如果等级相同，无影响。否则等级高的英雄等级+1。直到某个英雄等级到了100⁵⁰⁰游戏结束。问有多少个英雄最后可能获胜。

Solution

只要英雄等级不是最低的就有可能获胜。

Code

#include<iostream>
#include<cstdio>
#include <cmath>
#include <algorithm>
#define ll long long
const int maxn = 1e5 + 10;
int arr[maxn];
void solve()
{
    int n;
    scanf("%d", &n);
    int ans = 0;
    int minn = 100000000;
    for (int i = 1; i <= n; ++ i)
    {
        scanf("%d", &arr[i]);
        if(arr[i] < minn)
            minn = arr[i];
    }
    for (int i = 1; i <= n; ++i)
        if (arr[i] != minn)
            ans++;
    printf("%d
", ans);
}

int main()
{
    int t ;
    scanf("%d", &t);
    while(t --)
    {
        solve();
    }
    return 0;
}

B - The Great Hero

有一个n个点的圆环。A在n号点，B在1号点。A逆时针走，B顺时针走。如果A和B下一步是一个点，那么A走一步，B走两步。问经过K步后B在几号点

Solution

偶数个点，不会碰到一起。奇数个点B会多走 k/（n/2）步

Code

#include<iostream>
#include<cstdio>
#include <cmath>
#include <algorithm>
#define ll long long
const int maxn = 1e5 + 10;
int arr[maxn];
void solve()
{
    int n, k;
    scanf("%d %d", &n, &k);
    int ans = 0;
    k--;
    if(n % 2)
    {
        k += (k / (n / 2));
    }
    k++;
    k %= n;

    printf("%d
", k == 0 ? n : k);
}

int main()
{
    int t ;
    scanf("%d", &t);
    while(t --)
    {
        solve();
    }
    return 0;
}

C - Searching Local Minimum

n个人两两进行一场战斗。平局各加一分，获胜加3分，失败不影响。请安排这些对局的结果 s.t. 最终所有人的分相等而且平局的数量尽可能少

Solution

显然总共有 n*(n-1)/2 局，如果全是非平局，那么一人 (n-1)/2局，那么只有在n是奇数的情况下成立。不然必定有平局产生。

然后就按照每个人被分到多少局进行分配就好了。

Code

#include<iostream>
#include<cstdio>
#include <cmath>
#include <algorithm>
#define ll long long
const int maxn = 1e2 + 10;
int arr[maxn][maxn];
void solve()
{
    int n, k;
    scanf("%d", &n);
    int ans = 0;
    k--;
    if(n % 2)
    {
        for (int i = 1; i <= (n + 1) / 2; ++ i)
        {
            for (int j = 1; j <= (n - 1) / 2; ++ j)
            {
                arr[i][j] = 1;
            }
            for (int j = (n - 1) / 2 + 1; j <= n - i; ++ j)
            {
                arr[i][j] = -1;
            }
        }
        for (int i = (n + 1) / 2 + 1; i <= n; ++ i)
        {
            for (int j = 1; j <= n - i; ++ j)
            {
                arr[i][j] = 1;
            }
        }

    }
    else
    {
        for (int i = 1; i <= n - (n / 2 - 1); ++i)
        {
            for (int j = 1; j <= n / 2 - 1; ++j)
            {
                arr[i][j] = 1;
            }
            for (int j = n / 2; j <= n / 2; ++ j)
                arr[i][j] = 0;
            for (int j = n / 2 + 1; j <= n - i; ++j)
            {
                arr[i][j] = -1;
            }
        }
        for (int i = n - (n / 2 - 1) + 1; i <= n; ++ i)
        {
            for (int j = 1; j <= n - i; ++ j)
            {
                arr[i][j] = 1;
            }
        }
    }

    for (int i = 1; i <= n; ++ i)
    {
        for (int j = 1; j <= n - i; ++ j)
        {
            printf("%d ", arr[i][j]);
        }
    }
    puts("");
}

int main()
{
    int t ;
    scanf("%d", &t);
    while(t --)
    {
        solve();
    }
    return 0;
}

D - Pythagorean Triples

找到数对(a,b,c) 满足 c^2 = a^2 + b^2 && c = a^2 - b

Solution

两个式子联立或者打表都知道 a^2 = 2*b+1 && c = b+1

然后暴力判或者瞎调个终式（如下）出来。

 

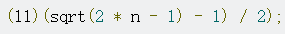
Code

#include<iostream>
#include<cstdio>
#include <cmath>
#include <algorithm>
#define ll long long
const int maxn = 1e2 + 10;
int arr[maxn][maxn];
int main()
{
    int t ;
    scanf("%d", &t);
    while(t --)
    {
        int n ;
        scanf("%d", &n);
        int ans = 0;
        for (int i = 3; i <= n; i +=2)
        {
            if (i * i / 2 + 1 <= n)
                ans++;
            else
                break;
        }
        printf("%d
", ans);
    }
    return 0;
}

E - Cheap Dinner

给定四个种类的菜各自的价格，给定一些关系：第一种菜中的某一种不能同时和第二种菜中的某一种一起被选中，然后2-nd和3-th，3-rd和4-th。

问四种菜中各择一的最小代价。

Solution

如果单考虑前两种，那么对于第二种菜中的所有菜，可以通过不同时被选中关系得到自己的最小代价（或者不能），把这个代价移到第二种菜上，2-nd和3-rd的菜之间的转移等价于1-st和2-nd之间的转移。一种类似DP转移的思想。代码实现方面就用multiset乱搞，每次考虑两种关系的时候，先把当前点所不连通的点删掉，最后再加回来，可以这么做的原因是我只要考虑值，不需要考虑具体的关系。

Code

#include <bits/stdc++.h>
using namespace std;
const int maxn = 2e5 + 10;
int arr[5][maxn], dp[5][maxn];
int nums[5];
vector<int> vv[5][maxn];
void solve()
{
    for (int i = 1; i <= 4; ++ i)
        scanf("%d", &nums[i]);
    for (int i = 1; i <= 4 ; ++ i)
    {
        for (int j = 1; j <= nums[i] ; ++ j)
        {
            scanf("%d", &arr[i][j]);
        }
    }
    for (int i = 2; i <= 4; ++ i)
    {
        int m;
        scanf("%d", &m);
        for (int j = 1, x, y; j <= m; ++j)
        {
            scanf("%d %d", &x, &y);
            vv[i][y].push_back(x);
        }
    }
    for (int i = 1; i <= nums[1]; ++ i)
    {
        dp[1][i] = arr[1][i];
    }
    for (int i = 2; i <= 4; ++i)
    {
        multiset<int> ss;
        for (int l = 1; l <= nums[i - 1]; ++l)
        {
            if (dp[i - 1][l] != -1)
                ss.insert(dp[i - 1][l]);
        }
        for (int j = 1; j <= nums[i]; ++j)
        {
            for (int k = 0; k < vv[i][j].size(); ++k)
            {
                int v = vv[i][j][k];
                if (dp[i - 1][v] != -1)
                    ss.erase(ss.find(dp[i - 1][v]));
            }
            if (ss.size() == 0)
                dp[i][j] = -1;
            else
                dp[i][j] = *ss.begin() + arr[i][j];

            for (int k = 0; k < vv[i][j].size(); ++k)
            {
                int v = vv[i][j][k];
                if (dp[i - 1][v] != -1)
                    ss.insert(dp[i - 1][v]);
            }
        }
    }
    int ans = -1;
    for (int i = 1; i <= nums[4]; ++ i)
    {
        if(dp[4][i] != -1)
        {
            if(ans == -1 || ans > dp[4][i])
                ans = dp[4][i];
        }
    }
    printf("%d
", ans);
}

int main()
{
    int t = 1;
    // scanf("%d", &t);
    while(t --)
    {
        solve();
    }
    return 0;
}