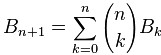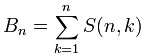错排数:D(n) = (n-1) [D(n-2) + D(n-1)], D(1) = 0, D(2) = 1
问题:n封信放入n个信封,要求全部放错方案数
解决方案:
假设n个元素的错排数记为D(n)
第一步,把第n个元素放在一个位置,比如位置k,一共有n-1种方法;
第二步,放编号为k的元素,这时有两种情况:⑴把它放到位置n,那么,对于剩下的n-1个元素,由于第k个元素放到了位置n,剩下n-2个元素就有D(n-2)种方法;⑵第k个元素不把它放到位置n,这时,对于这n-1个元素,有D(n-1)种方法;
综上得到:D(n) = (n-1) [D(n-2) + D(n-1)]。
斯特林数:
第一类斯特林数:
无符号:S(n, m) = S(n-1, m-1) + (n-1)*S(n-1, m), S(1, 1) = 1
问题:n个不同元素构成m个圆排列的方案数
解决方案:
如果第n个元素构成一个新的圆,那么方案数为S(n-1, m-1);
如果第n个元素和其他的元素构成圆,那么方案数为(n-1)*S(n-1, m)。
综上得到:S(n, m) = S(n-1, m-1) + (n-1)*S(n-1, m)。
有符号:S‘(n, m) = (-1) ^ (n+m) * S(n, m)
第二类斯特林数:S(n, m) = S(n-1, m-1) + m*S(n-1, m), S(n, n) = S(n, 1) = 1
问题:n个不同元素构成m个非空子集的方案数
解决方案:
如果第n个元素构成一个新的集合,那么方案数为S(n-1, m-1);
如果第n个元素和其他的元素构成集合,那么方案数为m*S(n-1, m)。
综上得到:S(n, m) = S(n-1, m-1) + m*S(n-1, m)。
贝尔数:
Bell数的定义:第n个Bell数表示集合{1,2,3,...,n}的划分方案数,B[0] = 1;
递推式:
卡特兰数:Cn = C(2n, n) - C(2n, n+1) = C(2n, n) / (n+1)