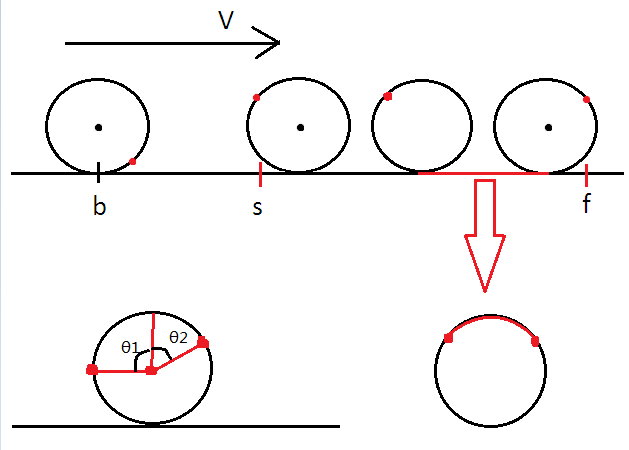
思路:开始和结束时的计时器的高度相同时(也就是关于圆竖着直径对称)时间最少。
证明:
总距离为d.
圆周长为s=2*π*r.
设len=d-floor(d/s)*s.
len=θ1*r+θ2*r+sin(θ1)*r+sin(θ2)*r.
要使sin(θ1)*r+sin(θ2)*r尽可能大,或者说θ1*r+θ2*r尽可能小。
根据和差化积公式的
sin(θ1)+sin(θ2)=2*sin((θ1+θ2)/2)*cos((θ1-θ2)/2)
(θ1-θ2)越趋近与0,值越大。
所以θ1=θ2=θ
所以变量只剩下一个变量θ了,而且函数是单调的,所以二分解三角函数。
代码:
#include<bits/stdc++.h> using namespace std; #define ll long long #define pb push_back #define mp make_pair #define pi acos(-1.0) #define pii pair<int,int> #define mem(a,b) memset(a,b,sizeof(a)) #define MAX(a,b,c) max(a,max(b,c)) const int INF=0x7f7f7f7f; const int MOD=1e9+7; const double eps=1e-6; int main() { /*ios::sync_with_stdio(false); cin.tie(0);*/ int n,r,v; scanf("%d%d%d",&n,&r,&v); double s=pi*r*2; while(n--) { int a,b; scanf("%d%d",&a,&b); double d=b-a; int c=(d/s); double len=d-c*s; double L=0,R=len; double mid=(L+R)/2; while(R-L>=eps) { if(mid+2*r*sin(mid/2/r)>=len)R=mid; else L=mid; mid=(L+R)/2; } printf("%.12lf ",(c*s+mid)/v); } return 0; }