之前介绍了有关PBR技术的一些理论知识,今天来讲一下利用代码如何实现相应的光照算法。
我们提到,我们最终要求解的其实就是这么一个积分:
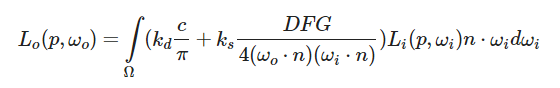
积分中kd的部分代表光照所产生的漫反射,ks的部分代表光照所产生的高光反射。如果充分考虑间接光照的效果(也就是从光源发射出光线后,不断碰撞反射,最终进入人眼),那这个积分事实上是极难求解的,但是我们可以先暂时不考虑间接光照,只考虑直接光照的部分。那么只需要在shader中,将所有的光源累加到该积分里就可以了,这个相对来说还是比较好做的。
我们首先把Cook-Torrance BRDF相关的代码实现一下(用HLSL实现),基本上就是对着公式写:
// 法向分布函数 N
float DistributionGGX(float3 N, float3 H, float roughness)
{
float pi = 3.14159265;
float a = roughness * roughness;
float a2 = a * a;
float NdotH = max(dot(N, H), 0.0);
float NdotH2 = NdotH * NdotH;
float num = a2;
float denom = (NdotH2 * (a2 - 1.0) + 1.0);
denom = pi * denom * denom;
return num / denom;
}
float GeometrySchlickGGX(float NdotV, float roughness)
{
float r = (roughness + 1.0);
float k = (r*r) / 8.0;
float num = NdotV;
float denom = NdotV * (1.0 - k) + k;
return num / denom;
}
//几何函数G
float GeometrySmith(float3 N, float3 V, float3 L, float roughness)
{
float NdotV = max(dot(N, V), 0.0);
float NdotL = max(dot(N, L), 0.0);
float ggx2 = GeometrySchlickGGX(NdotV, roughness);
float ggx1 = GeometrySchlickGGX(NdotL, roughness);
return ggx1 * ggx2;
}
//菲涅尔公式F
float3 fresnelSchlick(float cosTheta, float3 F0)
{
return F0 + (1.0 - F0) * pow(1.0 - cosTheta, 5.0);
}
然后具体的光照计算代码如下(以点光源为例,方向光原理):
void ComputePointLight(Material mat, PointLight light, float3 pos, float3 N, float3 V, float3 F0,
out float3 lo)
{
float3 L = light.Position - pos;
float distance = length(L);
// Range test.
if( distance > light.Range )
return;
// Normalize the light vector.
L /= distance;
float3 H = normalize(V + L);
float attenuation = 1.0 / (distance * distance);
float3 radiance = light.Diffuse.rgb * attenuation;
// cook-torrance brdf
float NDF = DistributionGGX(N, H, mat.roughness);
float G = GeometrySmith(N, V, L, mat.roughness);
float3 F = fresnelSchlick(max(dot(H, V), 0.0), F0);
float3 kS = F;
float3 kD = 1.0 - kS;
kD *= (1.0 - mat.metallic);
float3 numerator = NDF * G * F;
float denominator = 4.0 * max(dot(N, V), 0.0) * max(dot(N, L), 0.0);
float3 specular = numerator / max(denominator, 0.001);
float pi = 3.14159265;
float NdotL = max(dot(N, L), 0.0);
lo = (kD * mat.albedo / pi + specular) * radiance * NdotL;
}
上述代码中,V就是着色位置到相机的方向,N是法向,F0是前面提到的物体和菲涅尔效应有关的属性,lo是该光源在物体上最终产生的辐射。
材质的定义如下:
struct Material
{
float3 albedo;
float roughness;
float metallic;
};
其中albedo可以认为是物体本身的颜色,roughness就是粗糙度,metallic则是金属度。
PixelShader的代码如下所示:
float4 CustomPS(VertexOut pin,
uniform int gPointLightCount,
uniform int gDirLightCount,
uniform bool gUseShadowMap,
uniform bool gUseSSAO) : SV_Target
{
float3 color = float3(0.0f, 0.0f, 0.0f);
pin.NormalW = normalize(pin.NormalW);
float3 V = normalize(gEyePosW - pin.PosW);
V = normalize(V);
// 根据金属度计算物体的F0
float3 F0 = float3(0.04, 0.04, 0.04);
F0 = lerp(F0, gMaterial.albedo, gMaterial.metallic);
float3 L0 = float3(0.0, 0.0, 0.0);
float shadow = 1.0;
if (gUseShadowMap)
shadow = CalcShadowFactor(samShadow, gShadowMap, pin.ShadowPosH);
float ambient_weight = 1.0;
if (gUseSSAO)
{
pin.SSAOPosH /= pin.SSAOPosH.w;
ambient_weight = gSSAOMap.Sample(samLinear, pin.SSAOPosH.xy, 0.0f).r;
}
float3 ambient = gMaterial.albedo * 0.03 * ambient_weight;
//
// Lighting.
//
if (gPointLightCount + gDirLightCount > 0)
{
[unroll]
for (int i = 0; i < gDirLightCount; ++i)
{
float3 lo = float3(0.0, 0.0, 0.0);
ComputeDirectionalLight(gMaterial, gDirLights[i], pin.NormalW, V, F0, lo);
color += shadow * lo;
}
[unroll]
for (int i = 0; i < gPointLightCount; i++)
{
float3 lo = float3(0.0, 0.0, 0.0);
ComputePointLight(gMaterial, gPointLights[i], pin.PosW, pin.NormalW, V, F0, lo);
color += shadow * lo;
}
}
color += ambient;
if (enableHDR)
{
float exposure = max(0.0, HDRexposure);
color = 1.0 - exp(color * exposure);
}
if (gammaCorrection)
{
float gamma_ratio = 1.0 / 2.2;
color = pow(color, gamma_ratio);
}
return float4(color, 1.0);
}
基本计算过程就如上所示。最后展示一下不同粗糙度和金属度下渲染结果。
图中共有25个球,从左到右其粗糙度越来越大,从上到下其金属度越来越大。可以看到,随着粗糙度的增加,高光汇聚的亮度区域会越来越小;而随着金属度的增加,漫反射的部分也会越来越少。
