上一篇文章我们讲了Cook-Torrance BRDF模型,我们知道它由三个部分组成:法向分布函数、几何函数以及菲涅尔(Fresnel)公式。这次我们讲菲涅尔公式。
当光线碰撞到一个表面的时候,菲涅尔公式会返回被反射的光线所占的比例,根据能量守恒定律我们就可以相应地计算出折射的光线所占比。这种反射占比其实不仅和物体本身的材质有关,也和视线和物体本身的夹角有关。比如说,正对着看一个平面,看到的一定是只有很少的高光反射,但是如果从和平面近乎90°的角度观察的话,那么高光的占比就会非常明显。综合以上观察,用Fresnel-Schlick近似法求得菲涅尔公式的近似解:
(large{F_{Schlick}(h,v,F_0) = F_0 + (1 - F_0){(1-(ncdot v))}^5})
(F_0)表示平面的基础反射率,这是一个随材质而不同的参数,在一些数据库中可以查到不同材质的(F_0)值:
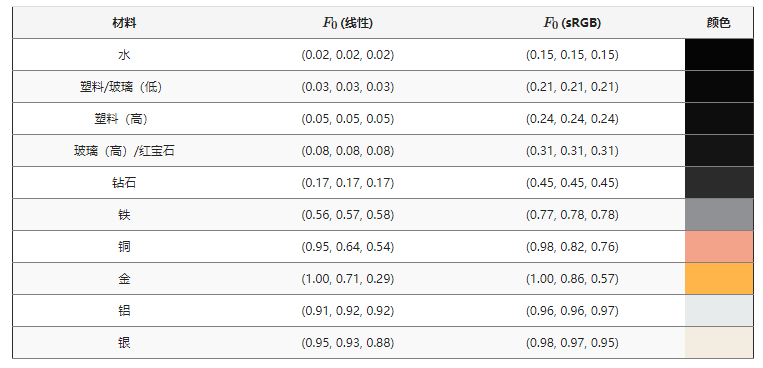
观察上表可以发现一个有趣的点:金属材料和非金属材料的(F_0)值是存在差异的,非金属材料的(F_0)三个通道的值一般不会高于0.17,金属材料则可能到1.0;另外非金属材料三个通道的值是不相等的,金属材料相反。因为金属和非金属在菲涅尔效应上的不同特性,物理学上将金属称为导体(Conductor),非金属称为电介质(Dielectric),所幸通过(F_0)我们可以将导体和电介质的菲涅尔效应用Fresnel-Schlick近似的公式统一起来。
在实际编码的时候,我们设定一个参数metalness,定义了物体材质的金属程度,通过它计算出(F_0)。
vec3 F0 = vec3(0.04);
F0 = mix(F0, surfaceColor.rgb, metalness);
如果是电介质,我们可以输入它自己的(F_0),对于金属则应用默认的0.04(一个经验值),然后根据metalness的值和物体自身的颜色做中和。也就是说,如果metalness为1,那么(F_0)完全用的是金属自己的颜色(此时只有高光反射,没有漫反射了)。
然后计算菲涅尔公式:
vec3 fresnelSchlick(float cosTheta, vec3 F0)
{
return F0 + (1.0 - F0) * pow(1.0 - cosTheta, 5.0);
}
其中cosTheta是表面法向量n与观察方向v的点乘的结果。
Cook-Torrance反射率方程
介绍完了菲涅尔公式之后,我们就可以得到最终的基于Cook-Torrance BRDF的反射方程:

可以看到反射方程中的(f_r)替换成了Cook-Torrance BRDF,另外ks其实就是菲涅尔公式的F,kd=(1-ks)(1-metalness),这是因为金属会更多的吸收折射光线导致漫反射消失,这是金属物质的特殊物理性质。
所以上面那个积分实际应该这么写:
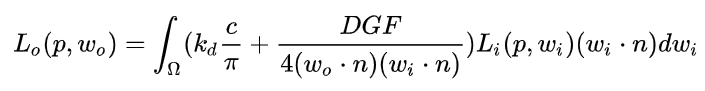
之后会探讨如何在实时渲染中求解该方程。