俄罗斯轮盘算法

在进行路径追踪时，一个要解决的问题是怎样以有限的资源来无偏估计具有无限长度路径的光照贡献。俄罗斯轮盘是解决这个问题的一种方法，它基于这样一种思路：对于物理正确的光照传输，长度越长的路径其反射的光照越小，因此可以将贡献量足够小的路径剔除掉。
为了应用俄罗斯轮盘，我们在每次要投射一条新的路径的时候，设定一个概率q，该路径有q的概率被终止，有1-q的概率被继续追踪，设F为已经计算出的蒙特卡洛估计值，那么：

一般来说，c=0。之所以要将F除以(1-q)是为了保证该估计的期望和原始估计的期望是相等的：

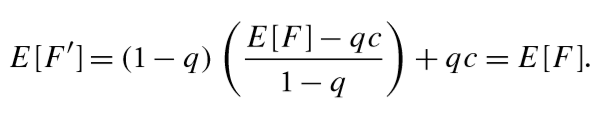
我们一般把q设为路径上基于BRDF的权重，权重越小则路径追踪越容易被终止。
俄罗斯轮盘不会减少估计的方差，但是可以提升估计的效率，可以叫停一些贡献很小的路径。
BRDF中对俄罗斯轮盘的实现如下所示,可以看到，首先BRDF用的是吞吐量的权重来衡量q值，其次并不是一开始就运用俄罗斯轮盘，而是在已经有三次反射以后才引入的：

beta *= (f * abs(DotFloat3(wi, it.normal))/pdf);

// Russian roulette
if (bounce > 3)
{
    float q = std::max<float>(0.05f, 1.0 - beta.y());
    if (generateRandomFloat() < q)
	break;
    beta /= (1.0 - q);
}