蒙特卡洛积分法（一）

今天我们来讲一节数学课：蒙特卡洛积分
一般在工程实践中，面对的函数千变万化，我们很难直接计算得出某个函数的积分的解析解。为了求解函数积分的数值解，蒙特卡洛法是一种强大的积分方法。它的推导过程如下：
假设我们想去求得函数g的积分，首先根据大数定理，任意给定一个实数函数f和随机变量x~p(x)，可以得到：

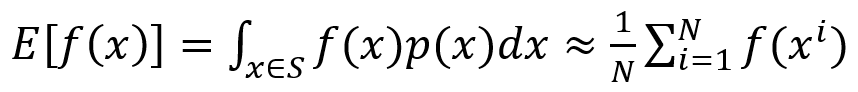
令g=fp，代换上式可得：

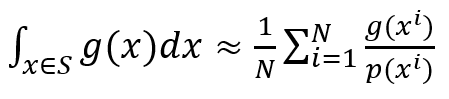
它的期望值为：

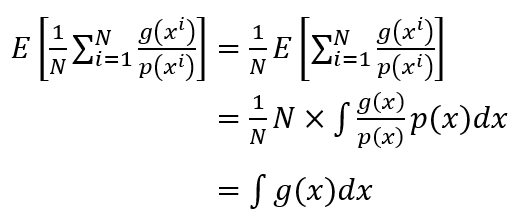
也就是说，当N取的足够大时，结果将无限逼近解析积分。
综上所述，蒙特卡洛方法是一种可以近似计算任意函数积分的数值方法。它的计算分为以下步骤：
1.对一个满足某种概率分布的随机数进行抽样
2.使用该抽样计算g(x)/p(x)的值，作为样本
3.最后对所有的样本累加求平均

写了一段代码来验证一下sin(x)在[0,pi]区间的积分，采用均匀分布：

import random
import math
count = 10000
sum = 0.0
pi = 3.14159265
for i in xrange(count):
	p = 1.0 / pi
	x = random.uniform(0.0, pi)
	sum += math.sin(x)/p
sum /= count
print sum
print math.cos(0) - math.cos(pi)

解析解为2，数值解为1.98730395714，可以说是很接近了。
用蒙特卡洛积分法求积分涉及到两个问题：1.如何对一个任意分布函数进行抽样； 2.如何减少方差，我们之后会对它进一步探讨。