2-1
视角1:
一般平方损失函数的公式如下图所示:
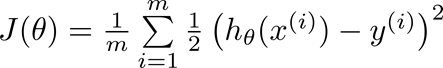
h表示的是你的预测结果,y表示对应的标签,J就可以理解为用二范数的方式将预测和标签的差距表示出来,
模型学习的过程就是优化权重参数,使得J达到近似最小值。
理论上这个损失函数是很有效果的,但是在实践中却又些问题。
它这个h是激活函数激活后的结果,激活函数通常是非线性函数,
例如sigmoid之类的,这就使得这个J的曲线变得很复杂,并不是凸函数,不利于优化,很容易陷入到局部最优解的情况。
视角2:
在使用One-Hot编码表示分类问题的真实标签的情况下,
我们使用平方损失函数计算模型的预测损失时会计算预测标签中每一个类别的可能性与真实标签之间的差距。
若我们想要得到更小的损失,则需要模型预测得到的预测标签整体与One-Hot编码的真实标签相近,这对于模型来说计算精度要求过高、
在分类我们上我们往往只关注模型对数据的真实类别的预测概率而不关注对其他类别的预测概率。
所以对分类问题来说,平方损失函数不太适用。
2-2

2-3

2-4

2-5
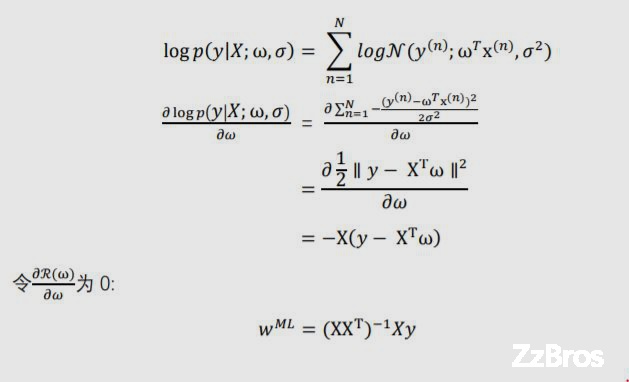
2-6

2-7

2-8[不懂...]

2-9
拟合能力强的模型一般复杂度会比较高,容易过拟合,方差比较高。
如果限制模型复杂度,降低拟合能力,可能会欠拟合,偏差比较高.
2-10
简单写:
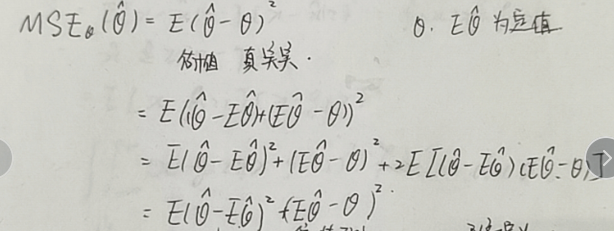
复杂写:

2-11

当n增长时,计算压力和参数空间会迅速增长。n越大,数据越稀疏。
2-12

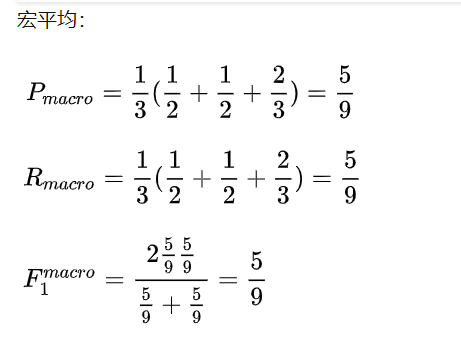

微平均其实就是所有类别的准确率。即(TP + TN) / (TP + FP + TN + FN)。