5、给定如表4-9所示的概率模型,求出序列a1a1a3a2a3a1 的实值标签。

解:由概率模型可知: Fx(1)=0.2 , Fx(2)= 0.5 , Fx(3)=1
由公式来确定标签所在区间的上下限。
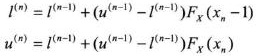
依次对序列1 11 113 1132 11323 113231 编码:
l(1)= l(0)+( u(0)- l(0)) Fx(0)=0+(1-0)*0=0
u(1)= l(0)+( u(0)- l(0)) Fx(1)= 0+(1-0)*0.2=0.2
l(11)= l(1)+( u(1)- l(1)) Fx(0)=0+(0.2-0)*0=0
u(11= l(1)+( u(1)- l(1)) Fx(1)= 0+(0.2-0)*0.2=0.04
l(113)= l(2)+( u(2)- l(2)) Fx(2)=0+(0.04-0)*0.5=0.02
u(113)= l(2)+( u(2)- l(2)) Fx(3)= 0+(0.04-0)*1=0.04
l(1132)= l(3)+( u(3)- l(3)) Fx(1)=0.02+(0.04-0.02)*0.2=0.024
u(1132)= l(3)+( u(3)- l(3)) Fx(2)=0.02+(0.04-0.02)*0.5=0.03
l(11323)= l(4)+( u(4)- l(4)) Fx(2)=0.024+(0.03-0.024)*0.5=0.027
u(11323)= l(4)+( u(4)- l(4)) Fx(3)=0.024+(0.03-0.024)*1=0.03
l(113231)= l(5)+( u(5)- l(5)) Fx(0)=0.027+(0.03-0.027)*0=0.027
u(113231)= l(5)+( u(5)- l(5)) Fx(1)=0.027+(0.03-0.027)*0.2=0.0276
由此可知标签包含在区间[0.0276,0.27)中。
根据公式
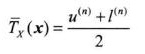
Tx(113231)=(0.0276+0.27)/2=0.0273
因此,序列a1a1a3a2a3a1的实值标签为0.0273 。
6、对于表4-9所示的概率模型,对于一个标签为0.63215699的长度为10的序列进行解码。
解:由概率模型可知:Fx(1)=0.2 , Fx(2)= 0.5 , Fx(3)=1
根据如图所示对标签为0.63215699的长度为10的序列的译码为 :
a3 a2 a2 a1 a2 a1 a3 a2 a3 a2。
