AGC 题解合集

开个坑，估计过段时间就弃了（）

由于是「题解合集」所以没有题面和代码。

施工进度（点击「✔」可以跳转）：

编号	A	B	C	D	E	F
AGC001			✔	✔	✔	✔
AGC002				✔	✔	✔
AGC003				✔	✔	✔
AGC004				✔	✔	✔
AGC005			✔	✔	✔	✔
AGC006			✔	✔	✔	✔
AGC007			✔	✔	✔	✔
AGC008					✔	✔
AGC009			✔	✔	✔	-
AGC010			✔	✔	✔	✔
AGC011			✔	✔	✔	✔
AGC012		✔	✔	✔	✔	✔
AGC013			✔	✔	✔	✔

---

AGC001

AGC001C Shorten Diameter

枚举直径中点然后暴力统计不需要删掉的个数即可。

AGC001D Arrays and Palindrome

考虑每个奇数会让边数少 \(1\)，所以如果有两个及以上的奇数就寄了。然后考虑整一个这样的构造：

奇数的情况是类似的。

AGC001E BBQ Hard

考虑组合意义，无非是从 \((-a_i,-b_i)\) 走到 \((a_j,b_j)\) 的方案数，直接按照组合意义写一个 dp 即可。

AGC001F Wide Swap

考虑令 \(q_{p_x}=x\)，然后操作会变成每次如果相邻两个 \(q\) 的差 \(\geq k\) 则可以交换。不难发现这相当于钦定了若干组 \(p_i<p_j\)，然后求字典序最小的 \(p\)。

然后我就不会了，写了个贪心拓扑排序发现过了，我也不会证正确性。

然后看题解看会了，正确做法是拓扑排序然后每次取最大的没有出度的点赋值。正确性可以考虑一个 \(\mathcal O(n^2)\) 的贪心做法：每次取出最小的未赋值的位置，然后把能到它的点提出来递归做，优化暴力模拟就是上述做法。

AGC002

AGC002D Stamp Rally

整体二分即可。

AGC002E Candy Piles

哈哈，被博弈杀了。

排序之后相当于去掉第一行或者去掉第一列。然后 \(f_{u,d}\) 表示用了 \(u\) 个行操作和 \(d\) 个列操作是否是先手赢，考虑一下组合意义发现相当于边框上都是 \(1\)，然后每个位置后继是上面一个和右边一个。

然后编了一个用平衡树维护 01 交替序列的做法，发现巨大多难写就开始自闭了。

看题解发现做法非常高妙。打表观察一下发现如果不是边框之类的 border case 我们都有 \(f_{u,d}=f_{u+1,d+1}\)。证明可以手画一下不一样的情况发现都不合法。于是 \(f_{0,0}=f_{x,x}\)，只需要找到最大的不在边框上的 \(x\) 算它的函数值即可，这个函数值可以 \(\mathcal O(1)\) 算。

AGC002F Leftmost Ball

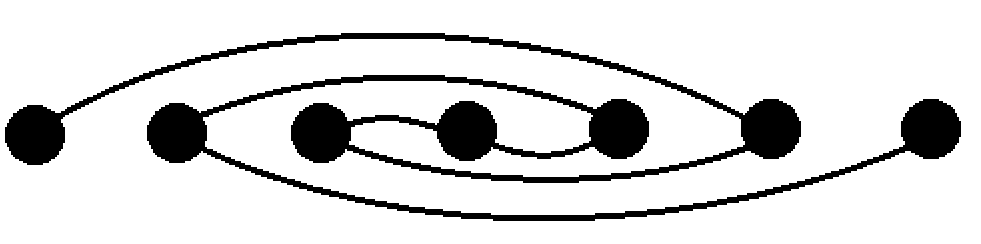
特判掉 \(k=1\) 的情况，剩下的情况先钦定第二个球的出现顺序是 \(1,2,3\cdots,n\)，最后只需要乘上 \(n!\)。然后注意到一个方案合法当且仅当第 \(i\) 个白球在第 \(i\) 个数第二次出现的位置前面，然后可以画出来这样一张图：

答案即往图里填排列使得 \(u\to v\) 则 \(p_u<p_v\) 的方案数。

注意到下面那一堆东西对答案的贡献只和第二排的点在前两排的相对位置有关，于是 \(dp_{i,j}\) 表示第一行考虑到了第 \(i\) 个数，第二行考虑到了第 \(j\) 个数即可。

AGC003

AGC003D Anticube

抄了个 PollardRho 过了。

看题解发现不需要真的分解出质因数。先筛掉 \(\leq \sqrt[3]{x}\) 的因子，然后剩余的至多有两个质因数，然后讨论一下发现可以 \(\mathcal O(1)\) 解决。

AGC003E Sequential operations on Sequence

发现只需要保留前缀单调栈当中的元素。然后维护一个序列 \(f\) 表示前 \(f_i\) 的数都出现了一次。剩下的注意到如果 \(x>m\) 则 \(x\bmod m\leq \frac x2\) 于是暴力维护 \(f\) 复杂度是对的。

AGC003F Fraction of Fractal

注意到如果矩形上下连通且左右连通则答案就是 \(1\)，如果两个都不是则答案是矩形个数，剩下的只需要考虑上下连通的情况。发现答案可以写成矩阵快速幂的形式，然后就做完了。

AGC004

AGC004D Teleporter

相当于定向成内向基环树。注意到如果环的大小 \(>1\) 就寄了，于是一定是 \(1\) 到自己，剩下的构成内向树。剩下的从底向上贪心即可。

AGC004E Salvage Robots

脑子不清醒想了一万年，冷静了一下突然会了。

看成是出口在动，其能任意访问而不产生任何影响的区域是一个矩形，把这个矩形记成状态，然后转移的时候是枚举扩展一步然后得到没被干掉的个数的贡献。

AGC004F Namori

笑死，根本想不到。

先考虑树的情况，二分图染色，把染色为 \(1\) 的位置翻转颜色，然后问题直接变成了移动所有黑色的棋子到指定的位置的最小代价，直接对每条边统计贡献即可。偶环的情况类似，只需要解一个 \(\min |x-a_i|\) 的方程，这个显然 \(x\) 取中位数最优。

奇环相当于每次可以用代价新生成两个黑色或者删除两个黑色，然后类似上面做即可。

AGC005

AGC005C Tree Restoring

把直径拿出来考虑即可。

AGC005D ~K Perm Counting

容斥，然后每条 \(\bmod k\) 的链独立，分开算最后多项式乘法即可。每条链可以 \(dp_{i,j,0/1,0/1}\) 表示考虑了前 \(i\) 个位置，有 \(j\) 个位置不合法，当前位置是否还没用，下一个位置是否还没用。

AGC005E Sugigma: The Showdown

哈哈，又被博弈杀了。

考虑 A 如果能走到一个在 B 树上相距超过 \(2\) 的边就 win 了。然后注意到一个关键性质是没走到之前 A 最多只能走长为 \(2\) 的边，这导致 A 始终无法跨过 B，于是 B 的最优策略就是每次朝着 A 走。那么 A 能到一个节点当且仅当它到 A 的距离小于到 B 的距离且它的所有父亲都可达。对所有能到的节点算一下即可。

AGC005F Many Easy Problems

F 比 E 简单系列。

对每个点考虑贡献，无非是 \(\binom ni-\sum_v {siz_v \choose i}\)，贡献是减法卷积的形式，多项式乘法即可。

AGC006

一场 AGC 出了 3 道联考题，一门三杰了属于是。

AGC006C Rabbit Exercise

注意到每次操作是交换差分数组。

AGC006D Median Pyramid Hard

二分答案，然后观察一下，发现形如 010101 的交错段每层都会往中间缩短 1，而形如 000111 的段是不变的。于是整个过程无非是距离中心最近的相同连续段把其他东西都干掉，找这个相同连续段即可。

AGC006E Rotate 3x3

每次操作是将 \(a,b,c\) 变成 \(-c,-b,-a\)。然后先把所有数归位，然后构造一下发现可以让两个距离为 \(2\) 的列同时取负：

\[a,b,c,d,e\\ -c,-b,-a,d,e\\ -c,-b,-e,-d,a\\ e,b,c,-d,a\\ e,b,-a,d,-c\\ a,-b,-e,d,-c\\ a,-b,c,-d,e \]

然后只用统计奇偶性即可。

AGC006F Blackout

三染色，即如果 \(u\to v\) 则 \(col_v=col_u+1\)。然后对每个连通块考虑一下可能发生的情况：

• 三染色失败，则会变成完全图
• 三染色成功，且三种颜色都存在，则会变成三分完全图
• 三染色成功，但没有三种颜色，则不变

然后对每个连通块算一下即可。

AGC007

AGC007C Pushing Balls

一个简单的想法是对每个位置算期望经过多少次，注意到第 \(2i-1\) 和第 \(2i\) 条线段的出现次数是一样的，所以一起记为 \(f_{i,j}\)。枚举第一次操作将这个东西递归到子问题，可以得到转移：

\[f_{i,j}=\frac{1}{2i}(1+(2(j-1)+1)f_{i,j-1}+(2(i-j)+1)f_{i-1,j}) \]

然后思路就偏向了以为 \(f\) 可以算，打了个表发现 \(f_{i,1}=\frac{i!!-(i-1)!!}{2^ii!}\)，然后就自闭了。转换思路发现题目保证了输入是个等差数列，这意味着 \(d_i+d_{2n-i}\) 是定值，然后注意到 \(f\) 也是对称的，于是其实只需要求 \(f\) 每一行的和。推一下转移发现是调和级数状物，暴力算即可。

AGC007D Shik and Game

单调队列优化 dp 即可。

AGC007E Shik and Travel

一个简单的想法是记录 \(f_{u,v}\) 表示在 \(LCA(u,v)\) 的子树当中进到 \(u\)，从 \(v\) 出去的最小代价，二分答案之后就只需要记录是否合法，于是转而对记录 \(f_{u,v}\) 表示在 \(u\) 的子树中进到 \(v\)，中间过程合法，出去时的最小代价，注意到不需要考虑顺序，于是只需要考虑 \(v\) 在较小的子树中的情况，于是合法的状态最多只有 \(\mathcal O(\min(siz_l,siz_r))\) 个，根据 dsu on tree 的分析，这个是 \(\mathcal O(n\log n)\) 的，转移的时候双指针暴力即可。

AGC007F Shik and Copying String

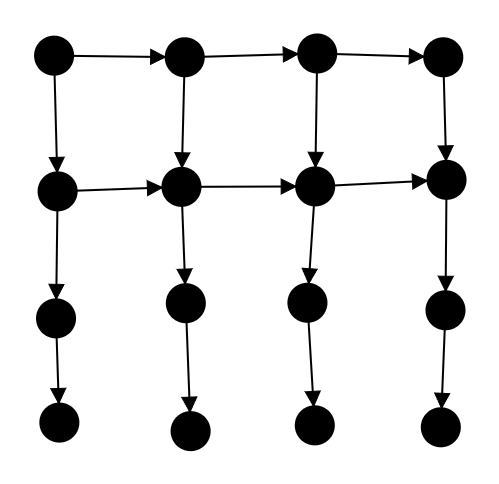
考虑整个过程，无非是下面的每个位置匹配一个上面的位置。

不难发现这个匹配一定是从后往前贪心匹配且中间每一层都贪心走能走到的最靠后的位置。注意到这个贪心每次相当于所有拐点向左下移动一格，于是用队列维护这个贪心的拐点即可。

AGC008

AGC008E Next or Nextnext

考虑从 \(i\) 向 \(a_i\) 连边，会构成内向基环树森林，猜一下结论：每个环在最终方案中的相对顺序不会变。手画一下发现除了这个环长为奇数且没有挂树有一种其他的方案，其他时候都是对的。

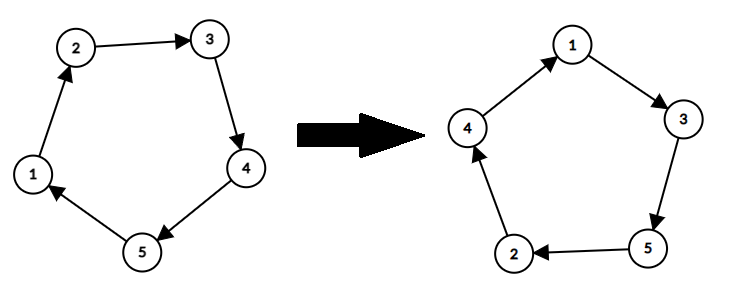
然后没有树的环还可以两个拼接在一起，剩下的只用考虑带树的环的方案数。可以看成是环上相邻两个位置之间可以填一个新的位置

注意到这时候每个树一定都是一条链，那么答案是容易计算的。

AGC008F Black Radius

考虑如果两个点的某个邻域相等则发现它们中间的链上的节点都存在一个邻域相等，上面还存在一个代表点，它的某个子树没有被选完

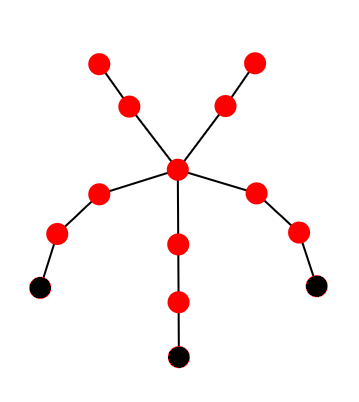
把直径中点提成根，那么这个代表点一定在这两个点到根的路上，换句话说，这时候我们每个点半径的可行范围是「是他的邻域且不是他的父亲的邻域」的所有半径，这是一个前缀，于是现在就能做所有点都是关键点的情况了。

存在某些点不是关键点的时候每个点还要求「是他的邻域且是某个关键点的邻域」的半径，注意到这个关键点一定在它的子树里，于是合法的是一段后缀，这个也是容易求的，求交即可得到每个点是一段区间，对区间长度求和即是答案。

AGC009

AGC009C Division into Two

假设 \(a>b\)，考虑所有 a 的位置。如果出现 aa 状的东西我们是不用管上一次 b 的出现位置的，否则一定是 ba，dp 即可。

AGC009D Uninity

问题等价于求层数最少的点分树。考虑类似 CF1444E 做，给每个点分配深度，方案合法当且仅当任意两个深度相同的点的路径上存在一个更浅的点。考虑贪心把每个点深度取成仅考虑子树的最小深度一定是最优的（证明同 CF1444E），于是可以把所有限制压成 int 维护，由于深度是 \(\mathcal O(\log n)\) 的，于是复杂度是对的。

AGC009E Eternal Average

发现两个东西会影响当且仅当产生了进位，那么 dp k 进制下的进位状况即可。

AGC010

AGC010C Cleaning

随便选一个不为叶子的节点做根，然后 \(f_{u,x}\) 表示给 \(u\) 上面接一个权值为 \(x\) 的叶子之后 \(u\) 的子树能不能行，然后合法的 \(x\) 显然是一段区间，那么直接维护这个东西。然后考虑一下每一层的转移，假设往上面接一个权值为 \(x\) 的叶子，那么合法当且仅当存在一个序列 \(b\) 满足

• \(b_i\in [l_i,r_i]\)
• \(\sum b_i+x=2a_u\)
• \(2\max (b_i,x)\leq \sum b_i+x\)

后面两个条件其实相当于限制了 \(b_i\leq a_u,x\leq a_u\)，前两个限制可以得到一个区间，取交集即可。

AGC010D Decrementing

被博弈杀+1

考虑如果没有除以 \(\gcd\) 则答案只和奇偶性相关，而除以奇数不会改变奇偶性。于是不难得到结论：如果某一时刻仅考虑奇偶性先手必胜则先手必胜，这是因为 \(n\geq 3\) 时先手总是可以让后手无法把所有数都变成偶数，\(n\leq 2\) 时简单讨论即可。

那么如果先手必败则先手一定需要除掉个偶数，否则后手必胜。那么必须是仅有一个奇数且不为 \(1\) 才行，也就是说只有一种决策，暴力递归这个决策。注意到每次递归会除以 \(2\)，于是复杂度是对的。

AGC010E Rearranging

被博弈杀+1，nmd 怎么全是博弈/fn

考虑如果已知了最终序列，则后手的策略是简单的：有若干个「x 必须在 y 前面」的限制，那么直接拓扑排序，每次贪心选最大值即可。

于是如果 \(\gcd(x,y)\neq 1\) 则连边 \((x,y)\)，先手的问题变成了给边定向成 DAG 使得最大拓扑序最小。对每个连通块分别考虑，假设它已经定向完成，则按照拓扑序取一外向生成树则构成一棵 DFS 树，于是最优的定向一定是某棵 DFS 树。发现不同 DFS 方式的影响只有环，而环上一定是贪心选较小的一边，那么直接每次选最小的未访问的出边一定是最优的。

最后模拟后手构造方案即可。

AGC010F Tree Game

我 杀 死 了 博 弈

为啥 AGC 永远是 E>>F 啊

这个对每个点求让人以为必有高论，但实际是在演。考虑 \(dp_u\) 表示仅考虑 \(u\) 的子树，从 \(u\) 出发能不能先手必胜。考虑一下转移，如果某个子树先手必胜则一定不会走这个子树，否则如果走过去那么后手的最优策略是走回来，原因是在那个子树里走没有前途。于是如果某个 \(a_v<a_u\) 则先手就能把后手耗死，否则先手就寄了，对每个点为根算一遍即可。

AGC011

AGC011C Squared Graph

UOJ#498 的弱化版，考虑对每对连通块算，假设分别是 \(G_1\) 和 \(G_2\)。那么首先如果 \(|G_1|=1\) 或 \(|G_2|=1\) 则为 \(|G_1||G_2|\)，否则考虑可以在两条边之间反复横跳，于是只需要考虑路径长度的奇偶性，即

• 如果 \(G_1\) 和 \(G_2\) 都是二分图则答案为 \(2\)
• 否则答案为 \(1\)

大力统计即可。

AGC011D Half Reflector

麻了，什么阴间找规律题

打个表发现如果第一个位置是 B 则会从右边出来，证明可以归纳。然后再观察一下发现每次从右边出来的效果都是循环移位一次然后全部取反，然后暴力模拟就可以 \(\mathcal O(k)\) 了。

然后找找规律发现循环节非常短，具体地，链长不超过 \(2n\)，环长是 \(1\) 或者 \(2\)，于是 \(k\) 被 reduce 到了 \(\mathcal O(n)\) 级别，暴力模拟即可。

证明考虑形如 ABABAB 的段不会被破坏且每轮都会产生，于是最多 \(2n\) 轮就会进入循环。

AGC011E Increasing Numbers

按照某个经典套路把上升的东西拆成不超过 \(9\) 个连续的 111111。假设用了 \(k\) 个这种东西，那么一定有

\[n=\sum_{i=1}^k \frac{10^{a_i}-1}{9}\\ 9n+k=\sum_{i=1}^k 10^{a_i} \]

也就是说合法的充要条件是 \(9n+k\) 的所有数位和小于等于 \(k\) 且和 \(k\) 在模 \(9\) 意义下相等，而答案是充分小的，直接枚举答案即可。

AGC011F Train Service Planning

设 \(X_i\) 表示去程在第 \(i\) 个站点停留的时间（\(i\in [0,n-1]\)），\(Y_i\) 表示返程在第 \(i\) 个站点停留的时间（\(i\in [1,n]\)），然后设 \(x_i\) 是 \(X_i\) 的前缀和，\(y_i\) 是 \(Y_i\) 的后缀和，\(S_a=\sum a_i\)，\(A_i\) 是 \(a_i\) 的前缀和，那么限制无非是

\[(x_i+A_{i-1},x_i+A_i)\cap (y_{i+1}+S_a-A_{i},y_{i+1}+S_a-A_{i-1})=\emptyset \]

注意到 \(2a_i>k\) 则无解，于是所有对条件的变换都是合法的。化简一下，无非是在模 \(k\) 意义下有

\[x_i-y_{i+1}\in [S_a-2A_{i-1},S_a-2A_{i}] \]

设 \(z_i=x_i-y_{i+1}\)，问题变成了如下的形式：

• 构造一个序列 \(z_{0\sim n-1}\)，满足 \(z_i\geq z_{i-1}\)，且 \(z_i\bmod k\in [l_i, r_i]\)
• 最小化 \(z_{n-1}-z_{0}\) 的值。

用 map 维护即可。

AGC012

AGC012B Splatter Painting

记录每个位置最后一次长为 \(d\) 的更新，然后枚举出边转移即可。

AGC012C Tautonym Puzzle

前面构造一个 \(1\sim m\)，后面构造一个 \(1\sim m\) 的排列，则个数即排列的最长上升子序列的个数。

AGC012D Colorful Balls

连成一张图然后每个连通块分别做即可。同色连边只用和最小值连，异色则只用暴力从全局最小值和和最小值颜色不同的最小值和第三小值暴力连所有点即可。

AGC012E Camel and Oases

显然只有 \(\mathcal O(\log V)\) 个不同的可行的值，问题相当于去掉这个区间之后左右两边能不能用剩下的干掉。枚举左边用掉了哪些长度，然后对这种东西求出左右两边能干掉的最多个数即可。

复杂度 \(\mathcal O(2^{\log V})=\mathcal O(V)\)

AGC012F Prefix Median

考虑如果所有元素不同怎么判断一个序列是否合法。

倒着考虑整个过程，于是每次操作是删除两个位置。要求变成了某次新的中位数和之前的中位数原本是相邻的。

那么首先注意到如果相邻两次分别是 \(i,j\)，那么 \((i,j)\) 区间内的一定已经删除了，而 \(j\) 一定还没有删除，于是可以得到每个位置删除时间的上下界，剩下的要求无非是每次删除的元素都合法（即和新的中位数不在同一侧），这个限制其实非常弱，只需要每次删除的东西在 \([a_{n-i},a_{n+i}]\) 即可满足。

于是变成了每次会增加两个合法位置，删除某些位置。只需要记录两边各有多少没有删除的位置即可转移，\(a\) 有相同的情况是类似的。

AGC013

AGC013C Ants on a Circle

根据链上的经典问题容易求出所有位置，只需要确定顺序。发现顺序不变，于是模拟出 1 所在的位置即可。

AGC013D Piling Up

我一开始的做法是钦定在 \([i,i+k]\) 当中然后答案就是 \(calc(k)-calc(k-1)\)，但这个做法需要求反射容斥斜率是 \(\frac 12\) 的情况然后就寄了。

正确做法是允许出现所有的起点但钦定一定有一个前缀和为 \(0\)，这样是容易转移的。

AGC013E Placing Squares

把贡献考虑成在区间中选两个数的方案数，于是只需要记录当前选了几个数，然后转移就是矩阵了。

AGC013F Two Faced Cards

考虑怎么判合法：当且仅当 \(\leq y_i\) 的个数不超过 \(i\)。

于是变成了：给出序列 \(f\) 和若干条线段，然后要求覆盖 \(i\) 的线段个数不能超过 \(f_i\)，要求选出最多的线段个数。询问无非是把序列的一段前缀减一，然后重新询问答案。

考虑如下的做法：最开始先从大到小考虑，每次不合法干掉左端点最小的，然后处理答案的时候从小到大考虑，每次不合法干掉右端点最大的。

后面那个贪心显然是对的，考虑一下为什么前半部分这么做能保证后半部分不会出现调整的情况。假设后半部分干掉了 \(s\)，而可以调整出 \(t\)，那么一定有：

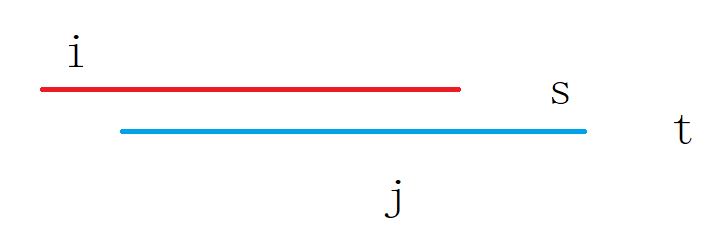
其中 \(j\) 是干掉 \(t\) 的位置。那么容易发现 \(i\) 一定在 \(t\) 的左端点前，\(j\) 一定在 \(s\) 的右端点前，于是在 \(j\) 的时候一定先干掉 \(s\) 而非 \(t\)，于是不合法。

扫两遍贪心即可。