题目大意 多组数据,每组数据给定一个正整数 (n(nleq 50)) 和平面内 (n) 个点,求出有多少个由这些点组成的简单,单调(monotone)多边形。一个单调多边形指的是构成这个多边形的所有边的斜率都在 ((-frac{pi}2,frac{pi}2)) 中。数据保证没有两个点 (x) 轴坐标相同。
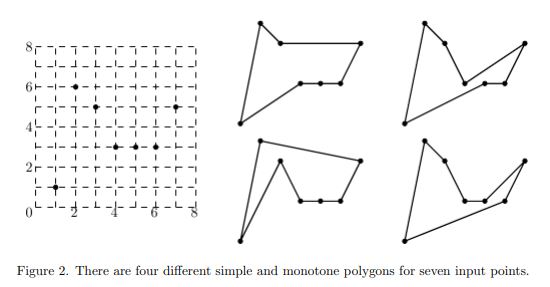
分析 不难想到将所有点按照 (x) 坐标排个序,然后按照上下两条折线考虑。我们令 (f[i][j](i eq j or i=j=1 or i=j=n)) 为上折线最右端为第 (i) 个点,下折线最右端为第 (j) 个点的所有方案数。不妨假定 (i<j),则 (f[i][j]) 只能向 (f[i][j+1]) 和 (f[j+1][j]) 转移。向 (f[i][j+1]) 的转移一定是可以的,我们来考虑向 (f[j+1][j]) 的转移。
用数学归纳法可以得到 (f[i][j]) 的所有方案数一定满足单调,那么就只用考虑简单了,也就是说边 ((i,j+1)) 不能和边 ((k, k+1)|i<k<j) 相交,也就是说点 (k|i<kleq j) 全都在边 ((i,j+1)) 的同一侧(下侧),更进一步,如果考虑点 (j+1) 的极角,有 (ang_i<ang_k(i<kleq j))。那么具体实现就很简单了。
最后要考虑到点 (n) 的转移,只能用 (f[i][n-1]) 或者 (f[n-1][j]) 来转移,那么分别用极角判定就可以了。
#include<bits/stdc++.h>
using namespace std;
const int maxn = 55;
const double PI = acos(-1);
int T, n;
int f[maxn][maxn];
struct Point {
int x, y;
inline bool operator<(Point d) const { return x < d.x; }
} p[maxn];
int main()
{
scanf("%d", &T);
while(T--) {
memset(f, 0, sizeof f);
scanf("%d", &n);
for(int i = 1; i <= n; ++i)
scanf("%d%d", &p[i].x, &p[i].y);
sort(p + 1, p + n + 1);
f[1][1] = 1;
for(int i = 1; i < n - 1; ++i) {
for(int j = 1; j < n - 1; ++j) {
if(i == j && i != 1) continue;
int now = max(i, j) + 1, pos;
bool whi = now == j + 1, flag = false;
if(!whi) pos = j, f[now][j] += f[i][j];
else pos = i, f[i][now] += f[i][j];
double ang = atan2(p[pos].y - p[now].y, p[pos].x - p[now].x);
if(ang < 0) ang += 2 * PI;
for(int k = min(i, j) + 1; k < now; ++k) {
double tmp = atan2(p[k].y - p[now].y, p[k].x - p[now].x);
if(tmp < 0) tmp += 2 * PI;
if((whi && tmp <= ang) || (!whi && tmp >= ang)) {
flag = 1;
break;
}
}
if(!flag) {
if(!whi) f[i][now] += f[i][j];
else f[now][j] += f[i][j];
}
}
}
double ang = atan2(p[n - 1].y - p[n].y, p[n - 1].x - p[n].x);
if(ang < 0) ang += 2 * PI;
for(int i = n - 2; i >= 1; --i) {
double tmp = atan2(p[i].y - p[n].y, p[i].x - p[n].x);
if(tmp < 0) tmp += 2 * PI;
if(tmp < ang) f[n][n] += f[i][n - 1];
ang = min(ang, tmp);
}
ang = atan2(p[n - 1].y - p[n].y, p[n - 1].x - p[n].x);
if(ang < 0) ang += 2 * PI;
for(int i = n - 2; i >= 1; --i) {
double tmp = atan2(p[i].y - p[n].y, p[i].x - p[n].x);
if(tmp < 0) tmp += 2 * PI;
if(tmp > ang) f[n][n] += f[n - 1][i];
ang = max(ang, tmp);
}
printf("%d
", f[n][n]);
}
}