斐波那契数列:
f(n)=f(n-1)+f(n-2)(n>2) f(0)=1;f(1)=1;
1 递归调用
public static long Fib(long N){
if (N == 0){
return 0;
} if (N < 3) return 1; else return Fib(N-1) + Fib(N-2); }
此种方法的缺陷:重复计算的次数太多,效率低
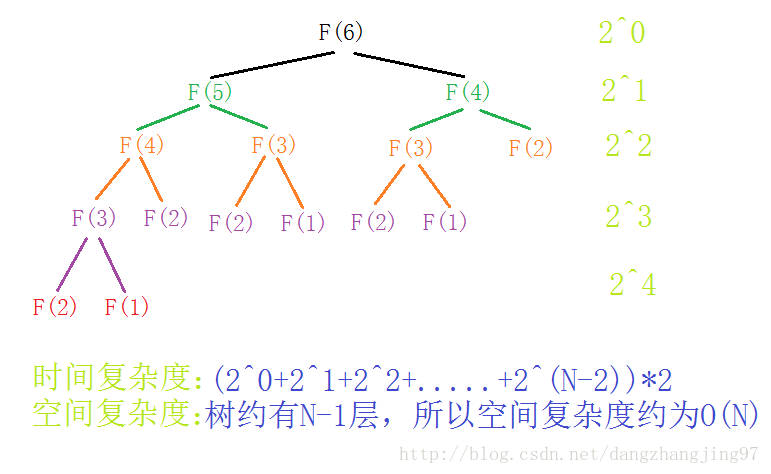
例如:在下图中,F(3)就重复计算了 "3次"
时间复杂度:O(2^N) 空间复杂度:O(N)
2 循环
public int Fibonacci(int n) { int first = 1; int second = 1; int ret = 1; if(n == 0){ return 0; } if(n < 3){ return 1; } for(int i = 3; i <= n ; i++){ ret = first + second; first = second; second = ret; } return second; }
时间复杂度:O(N)
空间复杂度:O(1)(创建了四个对象,是常数,所以可忽略不计)
此种方法是"最优方法"
优点:时间复杂度和空间复杂度最低,而且可读性高