归并排序
核心: 有序子列的归并
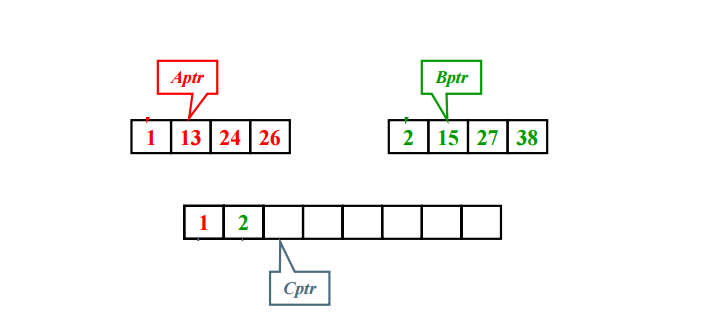
T(N) = O(N)
递归采用分治算法
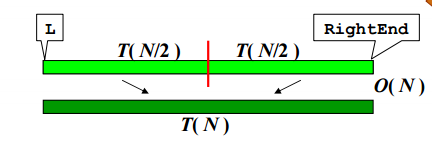
T(N) = T(N/2) + T(N/2) + O(N) -> T(N) = T(NlogN)
如果只在Merge中申请临时数组 会频繁申请释放空间 将耗费O(NlogN)的额外空间
所以只申请一个临时空间 只在临时空间的一段做操作 额外空间复杂度将保持O(N)
特点:
稳定 平均时间复杂度O(Nlog2N) 最坏时间复杂度O(Nlog2N) 额外空间复杂度O(N)
适合外部排序
代码:
1 #include <stdio.h> 2 #include <stdlib.h> 3 4 //归并函数 5 //将有序的A[L]~A[R-1]和A[R]~A[RightEnd]归并成一个有序序列 6 void Merge(ElementType A[], ElementType TmpA[], int L, int R, int RightEnd) 7 { 8 int LeftEnd, NumElements, Tmp; 9 int i; 10 11 LeftEnd = R-1; 12 NumElements = RightEnd - L + 1; 13 Tmp = L; //临时数组指针 14 15 while (L <= LeftEnd && R <= RightEnd) { 16 if (A[L] <= A[R]) 17 TmpA[Tmp++] = A[L++]; 18 else 19 TmpA[Tmp++] = A[R++]; 20 } 21 22 //复制剩余部分 23 while (L <= LeftEnd) 24 TpmA[Tmp++] = A[L++]; 25 while (R <= RightEnd) 26 TmpA[Tmp++] = A[R++]; 27 28 //TmpA复制回A 29 for (i = 0; i < NumElements; i++, RightEnd--) 30 A[RightEnd] = TmpA[RightEnd]; 31 } 32 33 //分治思想 核心递归排序函数 34 void Msort(ElementType A[], ElementType TmpA[], int L, int RightEnd) 35 { 36 int Center; 37 38 if (L < RightEnd) { 39 Center = (L+RightEnd) / 2; 40 Msort(A, TmpA, L, Center); 41 Msort(A, TmpA, Center+1, RightEnd); 42 Merge(A, TmpA, L, Center+1, RightEnd); 43 } 44 } 45 46 //归并排序 统一接口 47 void MergeSort(ElementType A[], int N) 48 { 49 ElementType *TmpA; 50 TmpA = (ElementType *)malloc(N*sizeof(ElementType)); 51 52 if (TmpA != NULL) { 53 Msort(A, TmpA, 0, N-1); 54 free(TmpA); 55 } 56 else printf("空间不足"); 57 }