Q1: 给出n个数,n<=100,和m个询问,每次询问区间[l,r]的和,并输出。
一种回答:这也太简单了,O(n)枚举搜索就行了。
另一种回答:还用得着o(n)枚举,前缀和o(1)就搞定。
那好,我再修改一下题目。
Q2: 给出n个数,n<=100,和m个操作,每个操作可能有两种:1、在某个位置加上一个数;2、询问区间[l,r]的和,并输出。
回答:o(n)枚举。
动态修改最起码不能用静态的前缀和做了。
好,我再修改题目:
Q3: 给出n个数,n<=1000000,和m个操作,每个操作可能有两种:1、在某个位置加上一个数;2、询问区间[l,r]的和,并输出。
回答:o(n)枚举绝对超时。
再改:
Q4: 给出n个数,n<=1000000,和m个操作,每个操作修改一段连续区间[a,b]的值
回答:从a枚举到b,一个一个改。。。。。。有点儿常识的人都知道超时
那怎么办?这就需要一种强大的数据结构:线段树。
1. 基本概念
- 线段树是一颗二叉搜索树,它存储的是一个区间的信息
- 每个节点以结构体的方式存储,结构体包含以下几个信息:区间左端点和右端点以及这个区间要维护的信息
- 线段树的基本思想:二分
- 线段树的一般结构如图所示
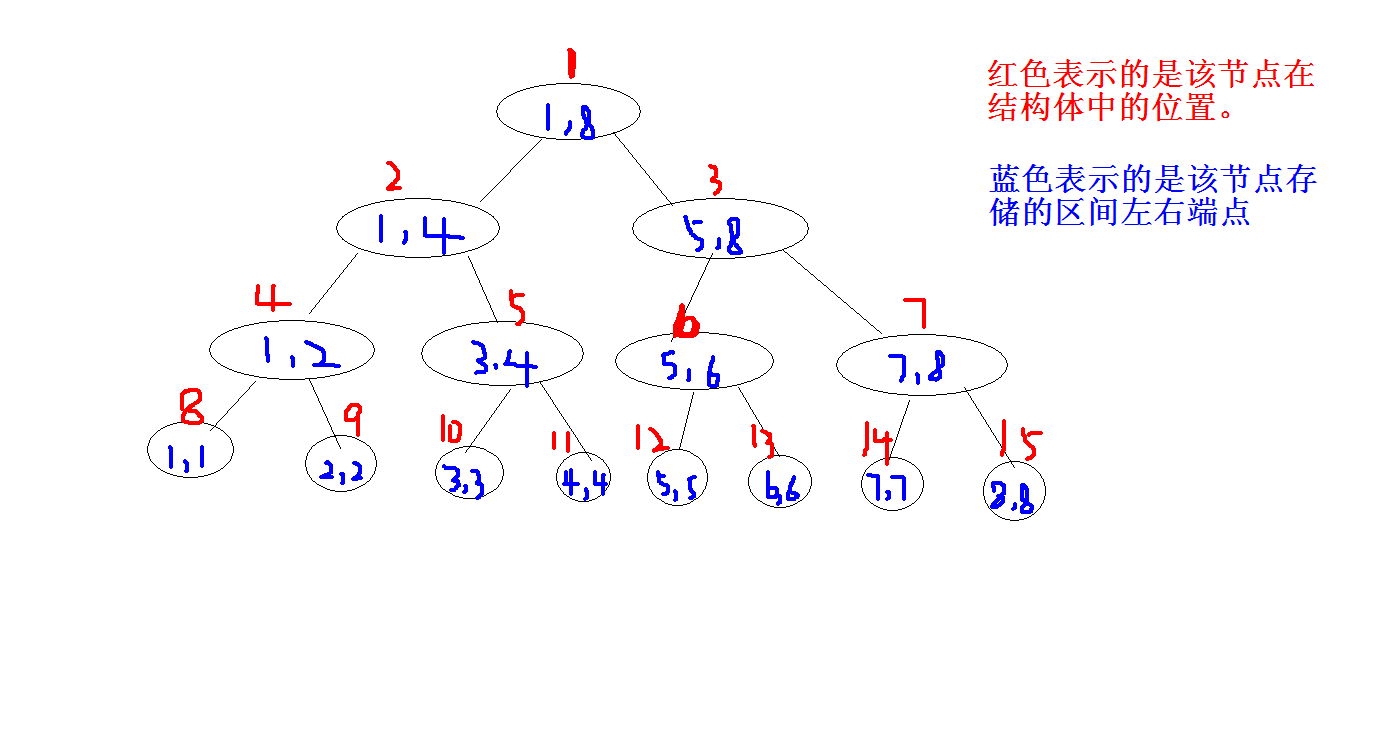
- 由上图可得,每个节点的左孩子区间范围为[1,mid],右孩子为[mid+1,r],对于节点k,左孩子节点是2k,右孩子节点是2k+1,完全符合二叉树的性质。