Tire树,即字典树,又称单词查找树或键树,是一种树型结构,是一种哈希树的变种。典型的应用是统计和排序大量的字符串(不仅限于字符串),所以经常被搜索引擎用于文本词频统计。它的优点是:最大限度地减少无畏的比较,查询效率比哈希表高。
Tire树的核心思想是空间换时间。利用字符串的公共前缀来降低查询时间的开销以达到提高效率的目的。Tire树的缺点是内存消耗非常大。
1. Trie树的性质
根节点不包含字符,每条边代表一个字符。
从根节点到某一节点,路径上经过的字符连接起来为该节点对应的字符串。
每个节点的所有子节点包含的字符都不相同
2. Trie树的构建
Trie树的键不是直接保存在节点中,而是由节点在树中的位置决定。一个节点的所有子孙都有相同的前缀(prefix),从根节点到当前结点的路径上的所有字母组成当前位置的字符串,结点可以保存当前字符串、出现次数、指针数组(指向子树)以及是否是结尾标志等等。
public TrieNode{
int num;//单词前缀出现的次数
TrieNode next[26];//指向子树的节点
boolean exist;//标记是否此处构成单词
}
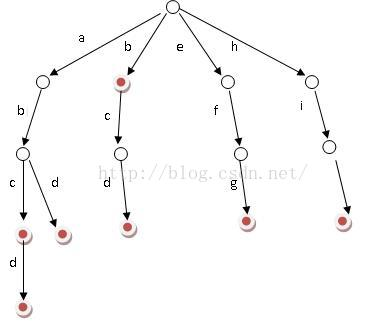
3.Trie树的基本操作
3.1 插入操作
/**
@para tire:数字的行代表节点的插入顺序值,列代表子节点(如果是小写字母的话是26个)
@para st:要插入的字符串
@para num:维持的一个节点序号
@para isword:判断当前节点是否构成单词
**/
public void Insert(String st,int index){
for(int i=0;i<st.length();i++){
int x = Integer.valueOf(st.charAt(i)-'a');
if(tire[index][x]==0) tire[num][x]=++num;//如果插入的字母在之前未出现则插入
index = tire[index][x];为下一个字母的插入做准备
}
isword[index]=true;标记该字母是否是单词的尾节点
}
3.2 查找操作
public boolean find(String st,int index){
for(int i=0;i<st.length();i++){
int x = Integer.valueOf(st.charAt(i)-'a');
if(tire[index][x]==0) return false;
index = tire[index][x];
}
return true;
//查询整个单词时,return isword[index];
}
3.3 查询前缀出现次数
/**
@para tire:数字的行代表节点的插入顺序值,列代表子节点(如果是小写字母的话是26个)
@para st:要插入的字符串
@para num:维持的一个节点序号
@para isword:判断当前节点是否构成单词
@para sum:存储当前节点的前缀被访问的次数
**/
public void Insert(String st,int index){
for(int i=0;i<st.length();i++){
int x = Integer.valueOf(st.charAt(i)-'a');
if(tire[index][x]==0) tire[num][x]=++num;//如果插入的字母在之前未出现则插入
index = tire[index][x];为下一个字母的插入做准备
sum[index]++;
}
isword[index]=true;标记该字母是否是单词的尾节点
}
public int search(){
root=0;
len=strlen(s);
for(int i=0;i<len;i++)
{
int id=s[i]-'a';
if(!trie[root][id]) return 0;
root=trie[root][id];
}//root经过此循环后变成前缀最后一个字母所在位置的后一个位置
return sum[root];//因为前缀后移了一个保存,所以此时的sum[root]就是要求的前缀出现的次数
}
4. Trie树的应用
4.1 字符串检索,词频统计,搜索引擎的热门查询
实现将已知的一些字符串(字典)的有关信息保存到trie树里,查找另外一些未知字符串是否出现过或者出现频率。举例如下:
1、有一个1G大小的一个文件,里面每一行是一个词,词的大小不超过16字节,内存限制大小是1M。返回频数最高的100个词。
2、给出N 个单词组成的熟词表,以及一篇全用小写英文书写的文章,请你按最早出现的顺序写出所有不在熟词表中的生词。
3、给出一个词典,其中的单词为不良单词。单词均为小写字母。再给出一段文本,文本的每一行也由小写字母构成。判断文本中是否含有任何不良单词。例如,若rob是不良单词,那么文本problem含有不良单词。
4、1000万字符串,其中有些是重复的,需要把重复的全部去掉,保留没有重复的字符串。请怎么设计和实现?
5、一个文本文件,大约有一万行,每行一个词,要求统计出其中最频繁出现的前10个词,请给出思想,给出时间复杂度分析。
6、寻找热门查询:搜索引擎会通过日志文件把用户每次检索使用的所有检索串都记录下来,每个查询串的长度为1-255字节。假设目前有一千万个记录,这些查询串的重复读比较高,虽然总数是1千万,但是如果去除重复和,不超过3百万个。一个查询串的重复度越高,说明查询它的用户越多,也就越热门。请你统计最热门的10个查询串,要求使用的内存不能超过1G(京东笔试题简答题与此类似)。
4.2 字符串最长公共前缀
trie树利用多个字符串的公共前缀来节省存储空间,反之,当我们把大量字符串存储到一棵trie树上时,我们可以快速得到某些字符串的公共前缀。举例:
- 给出N 个小写英文字母串,以及Q 个询问,即询问某两个串的最长公共前缀的长度是多少. 解决方案:
首先对所有的串建立其对应的字母树。此时发现,对于两个串的最长公共前缀的长度即它们所在结点的公共祖先个数,于是,问题就转化为了离线(Offline)的最近公共祖先(Least Common Ancestor,简称LCA)问题。
而最近公共祖先问题同样是一个经典问题,可以用下面几种方法:
-
利用并查集(Disjoint Set),可以采用经典的Tarjan 算法;
-
求出字母树的欧拉序列(Euler Sequence )后,就可以转为经典的最小值查询(Range Minimum Query,简称RMQ)问题了;
4.3 字符串排序
Trie树是一棵多叉树,只要先序遍历整棵树,输出相应的字符串便是按字典序排序的结果。
举例:给你N 个互不相同的仅由一个单词构成的英文名,让你将它们按字典序从小到大排序输出。
4.4 作为其他数据结构和算法的辅助结构
如后缀树,AC自动机等。
4.5 与hash表相比
优点:
trie数据查找与不完美哈希表(链表实现)在最坏情况下更快;对于trie树,最差为O(m),m为查找字符串的长度;对于不完美哈希表,会有键值冲突(不同键哈希相同),最坏为O(N),N为全部字符产生的个数。典型情况是O(m)用于哈希计算,O(1)用于数据查找。
trie中不同键没有冲突
trie的桶与哈希表用于存储键冲突的桶类似,仅在单个键与多个值关联时需要
当更多的键加入到trie中,无需提供hash方法或改变hash方法
trie通过键为条目提供字母顺序
缺点:
trie数据查找在某些情况下(磁盘或随机访问时间远远高于主存)比哈希表慢
当键值为某些类型(如浮点型),前缀链很长且前缀不是特别有意义。
一些trie会比hash表更消耗内存。对于trie,每个字符串的每个字符都要分配内存;对于大多数hash,只需要为整个条目分配一块内存。
4.6 与二叉搜索树相比
二叉搜索树,又称二叉排序树,它满足:
任意节点如果左子树不为空,左子树所有节点的值都小于根节点的值;
任意节点如果右子树不为空,右子树所有节点的值都大于根节点的值;
左右子树也都是二叉搜索树;
所有节点的值都不相同。
其实二叉搜索树的优势已经在与查找、插入的时间复杂度上了,通常只有O(log n),很多集合都是通过它来实现的。在进行插入的时候,实质上是给树添加新的叶子节点,避免了节点移动,搜索、插入和删除的复杂度等于树的高度,属于O(log n),最坏情况下整棵树所有的节点都只有一个子节点,完全变成一个线性表,复杂度是O(n)。
Trie树在最坏情况下查找要快过二叉搜索树,如果搜索字符串长度用m来表示的话,它只有O(m),通常情况(树的节点个数要远大于搜索字符串的长度)下要远小于O(n)。