TensorFlow实现自编码器及多层感知机

1 自动编码机简介

       传统机器学习任务在很大程度上依赖于好的特征工程，比如对数值型，日期时间型，种类型等特征的提取。特征工程往往是非常耗时耗力的，在图像，语音和视频中提取到有效的特征就更难了，工程师必须在这些领域有非常深入的理解，并且使用专业算法提取这些数据的特征。

       深度学习则可以解决人工难以提取有效特征的问题，它可以大大缓解机器学习模型对特征工程的依赖。深度学习在早起甚至被认为是一种无监督的特征学习，模仿了人脑的对特征逐层抽象提取的过程。这其中有两点比较重要：一是无监督学习，即我们不需要标注数据就可以对数据进行一定程度的学习，这种学习是对数据内容的组织形式的学习，提取出频繁出现的特征；二是逐层抽象，特征是需要不断抽象的，就像人总是从简单基础的概念开始学习，再到复杂的概念。学生们要从加减乘除开始学起，再到简单函数，然后到微积分，深度学习也一样，它从简单的微观的特征开始，不断抽象特征的层级，逐渐往复杂的宏观特征转变。

       特征是可以不断抽象转为高一级的特征的，那我们如何找到这些基本结构然后抽象呢？如果我们有很多标注数据，则可以训练一个深层的神经网络。如果没有标注的数据呢？在这种情况下，我们可以使用无监督的自编码器来提取特征。自编码器(AutoEncoder)，使用自身的高阶特征编码自己。自编码器其实也是一种神经网络，它的输入和输出是一致的，它借助稀疏编码的思想，目标是使用稀疏的一些高阶特征重新组合来重构自己。因此，它的特点很明显：第一，期望输入/输出一致；第二，希望使用高阶特征来重复自己，而不是复制原像素点。，所以我们对自编码器加入了集中限制：

       （1）如果限制中间隐藏层节点的数量，比如让中间隐藏层节点的数量小于输入/输出节点的数量，就相当于是一个降维的过程。此时已经不可能出现复制所有节点的情况，只能学习数据中最重要的特征复原，将可能不太相关的内容去除。

       （2）如果给数据加入噪声，那么就是Denoising AutoEncoder(去噪自编码器)，我们将从噪声中学习出数据的特征。同样的我们也不可能完全复制节点，完全复制并不能去除我们添加的噪声，无法完全复原数据。所以唯有学习数据频繁出现的模式和结构，将无规律的噪声略去，才可以复原数据。

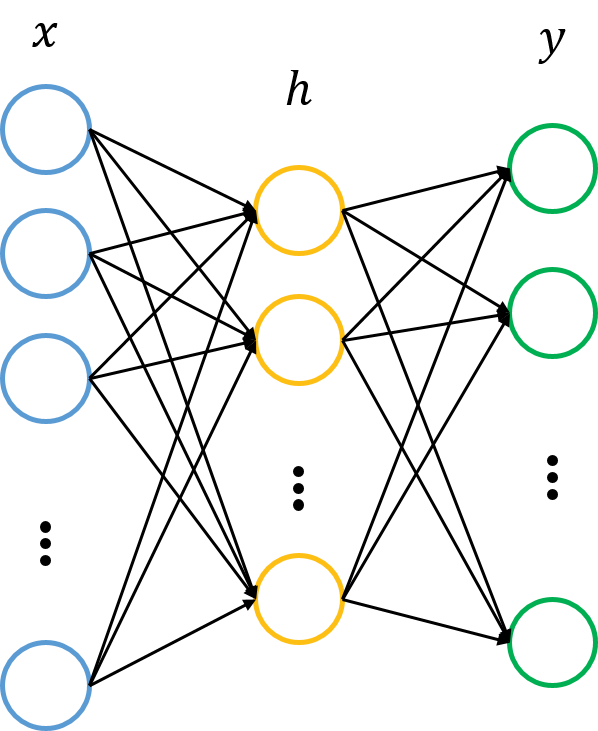
自编码器图示

2 实现一个自编码器

import os
os.environ['TF_CPP_MIN_LOG_LEVEL']='2'
import numpy as np
import sklearn.preprocessing as prep
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data

def xavier_init(fan_in,fan_out,constant=1):#根据某一层网络的输入/输出节点数量自动调整最合适的分布
    low = -constant*np.sqrt(6.0/(fan_in+fan_out))
    high = -constant*np.sqrt(6.0/(fan_in+fan_out))
    return tf.random_uniform((fan_in,fan_out),minval=low,maxval=high,dtype=tf.float32)

class AdditiveGaussianNoiseAutoencoder(object):#去噪自编码器的定义
    def __init__(self,n_input,n_hidden,transfer_function=tf.nn.softplus,optimizer=tf.train.AdamOptimizer(),scale=0.1):
        self.n_input=n_input
        self.n_hidden=n_hidden
        self.transfer=transfer_function
        self.scale=tf.placeholder(tf.float32)
        self.training_scale=scale
        network_weights=self.initialize_weights()
        self.weights=network_weights

        self.x=tf.placeholder(tf.float32,[None,self.n_input])#输入层
        self.hidden = self.transfer(tf.add(tf.matmul(self.x+scale*tf.random_normal((n_input,)),self.weights['w1']),self.weights['b1']))#隐藏层
        self.reconstruction = tf.add(tf.matmul(self.hidden,self.weights['w2']),self.weights['b2'])#重建层

        self.cost = 0.5*tf.reduce_sum(tf.pow(tf.subtract(self.reconstruction,self.x),2.0))#损失函数
        self.optimizer = optimizer.minimize(self.cost)#最优化损失函数

        init = tf.global_variables_initializer()
        self.sess = tf.Session()
        self.sess.run(init)

    def initialize_weights(self):#初始化参数
        all_weights = dict()
        all_weights['w1'] = tf.Variable(xavier_init(self.n_input,self.n_hidden))
        all_weights['b1'] = tf.Variable(tf.zeros([self.n_hidden],dtype=tf.float32))
        all_weights['w2'] = tf.Variable(tf.zeros([self.n_hidden,self.n_input],dtype=tf.float32))
        all_weights['b2'] = tf.Variable(tf.zeros([self.n_input],dtype=tf.float32))

        return all_weights

    def partial_fit(self,X):#训练+损失值计算
        cost,opt=self.sess.run((self.cost,self.optimizer),feed_dict={self.x:X,self.scale:self.training_scale})
        return cost

    def calc_total_cost(self,X):#只计算损失值
        return self.sess.run(self.cost,feed_dict={self.x:X,self.scale:self.training_scale})

    def transform(self,X):#隐藏层
        return self.sess.run(self.hidden,feed_dict={self.x:X,self.scale:self.training_scale})

    def reconstruct(self,X):#重构层
        return self.sess.run(self.reconstruction,feed_dict={self.x:X,self.scale:self.training_scale})

    def getWeights(self):#参数的获取
        return self.sess.run(self.weights['w1'])

    def getBiases(self):
        return self.sess.run(self.weights['b1'])

def standard_scale(X_train,X_test):
    preprocessor =  prep.StandardScaler().fit(X_train)
    X_train = preprocessor.transform(X_train)
    X_test = preprocessor.transform(X_test)
    return X_train,X_test
def get_random_block_from_data(data,batch_size):
    start_index = np.random.randint(0,len(data)-batch_size)
    return  data[start_index:(start_index+batch_size)]

if __name__=='__main__':
    mnist = input_data.read_data_sets("MNIST_data",one_hot=True)
    X_train,X_test = standard_scale(mnist.train.images,mnist.test.images)

    n_samples = int(mnist.train.num_examples)
    training_epochs = 20
    batch_size = 128
    display_step = 1
    autoencoder = AdditiveGaussianNoiseAutoencoder(n_input=784,n_hidden=200,transfer_function=tf.nn.softplus,optimizer=tf.train.AdamOptimizer(learning_rate=0.001),scale=0.01)

    for epoch in range(training_epochs):
        avg_cost=0
        total_batch = int(n_samples/batch_size)
        for i in range(total_batch):
            batch_xs = get_random_block_from_data(X_train,batch_size)

            cost = autoencoder.partial_fit(batch_xs)
            avg_cost += cost/n_samples * batch_size

        if epoch%display_step==0:
            print("Epoch:",'%04d' % (epoch+1), "cost=","{:.9f}".format(avg_cost))

    print ("Total cost:"+str(autoencoder.calc_total_cost(X_test)))

3 多层感知机简介

在之前我们使用tensorflow实现了一个简单的Softmax Regression模型，这个线性模型虽然好用但是拟合能力不强，可以算作是多分类问题的逻辑回归，它和传统神经网络的最大区别是没有隐含层。隐含层是神经网络中的一个重要概念，它 是指除了输入/输出外的那些层。

过拟合是机器学习的一个常见问题，它是指模型准确率在训练集上升高，但是在测试集上下降，这通常意味着泛化性能不好，模型只记忆了当前数据的特征，不具备推广能力。为了解决这一问题，Hinton提出了一个简单有效的方法，Dropout，使用复杂的卷积神经网络尤其有效，它的大致思路是在训练时，将神经网络某一层的节点随机丢弃一部分。这种做法实际上等于创造了更多的训练数据，通过增大样本量，减少特征数量来防止过拟合。

参数调试是机器学习的另一大痛点，尤其是SGD的参数，对SGD设置不同的学习速率，最后得到的结果可能差异巨大。对SGD，一开始我们希望学习速率大一些，可以加速收敛，但是在训练后期又希望学习速率小一些，这样可以稳定的落在局部最优解上。不同的机器学习算法所需要的学习速率也不太好设置，需要反复调试，因此像Adagrad，Adam，Adadelta等自适应的方法可以减轻调试参数的负担。

梯度弥散是另一个影响深层神经网络训练的问题，在ReLU激活函数出现之前，神经网络训练都是使用sigmoid作为激活函数。这可能是因为sigmoid函数具有限制性，输出结果在0~1，符合概率的定义。当神经网络的层数较多时，sigmoid函数在反向传播中梯度值会逐渐变小，经过多层传输后悔呈指数级减少，因此梯度在传到前面几层是就变得很小，这种情况下神经网络的参数更新将会很慢。知道ReLu的出现才解决了这个问题，ReLU是一个简单的非线性函数y=max(0,x),非常类似于人脑的阈值响应机制。信号在超过某个阈值是，神经元才进入兴奋状态，平时则处于抑制状态。

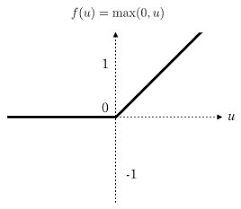
ReLU激活函数