这种有限制的类棋盘着色问题一般可以用指数型母函数来解决,设Hn表示这样的着色数,首先H0=1,则Hn等于四个字母的(A,B,C,D)的多重集合的n排列数,其中每个字母的重数是无穷,且要求A,C出现的次数是偶数,因此,H0,H1,...Hn,...的指数生成函数是A,B,C,D因子的乘积:
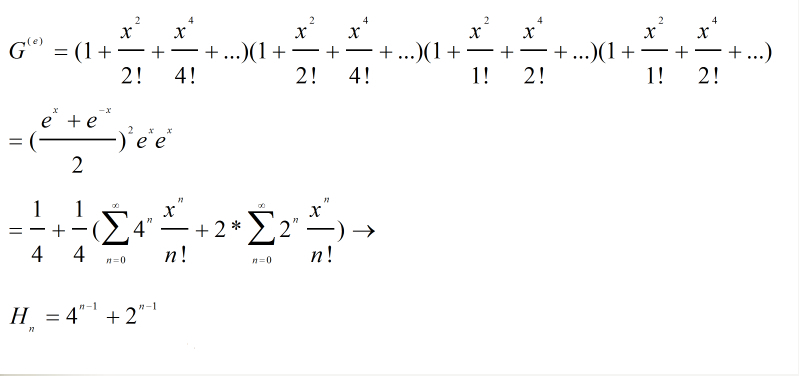
用快速幂解决,只不过在HDU不能用long long解决,要用__int64.
代码:

#include <iostream> #include <cstdio> #include <cstring> #include <cmath> #include <algorithm> #define lll __int64 #define ll long long using namespace std; #define N 250007 int fastm(int a,ll b,int m) { int t=1; while(b) { if(b&1LL) t=(t*a)%m; b >>= 1; a=(a*a)%m; } return t; } int main() { int t,i; ll n; int cs; while(scanf("%d",&t)!=EOF && t) { cs = 1; while(t--) { scanf("%I64d",&n); int res = fastm(4,n-1LL,100) + fastm(2,n-1LL,100); res %= 100; printf("Case %d: %d ",cs++,res); } puts(""); } return 0; }
