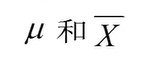1.什么是统计学,什么是描述统计,什么是推断统计
统计学(statistics):收集、处理、分析、解释数据并从数据中得出结论的科学。
描述统计(discriptive statistics)
描述统计(discriptive statistics):研究的是数据收集、处理、汇总、图表描述、概括与分析等统计方法。
描述统计其实就是对数据进行总体特征的概述,例子:说一下班级这次考试的情况如何
推断统计(inferential statistics)
推断统计(inferential statistics):是研究如何利用样本数据来推断总体特征的统计方法
推断统计其实是建立在描述统计的基础之上,在对总体数据有了大致的了解之后,运用一些分析方法,对数据进行预测,并达到统计决策的目的,其实不管是在统计学上,还是在实际的业务分析中,我们做分析的终极目的就是用来得出我们结论,应用于决策。例如:房价预测,通过预测数据来进行销售,用户看到房价走势,如果一路走高,是不是要提早下手。
2.统计研究的步骤
1、设计
全过程最关键的一步,良好的开端是成功的一半 选题--明确研究目的--提出假设--明确总体范围--确立观察指标--控制研究中的偏移--给出具体的研究方案
2、收集
收集数据,来源数据库,问卷等
3、整理
数据整理非常重要,现在的数据处理工具也比较好用,一定要把数据清洗干净,数据清洗好了才能得出正确的结论
4、分析
统计描述:了解样本数据的情况,是全部工作的基础,是尽量精确、直观而全面的对所获得的样本进行呈现
统计推断:从样本信息外推到总体,以获得对所感兴趣问题的解答
参数估计:样本---->所在总体特征
3.描述统计
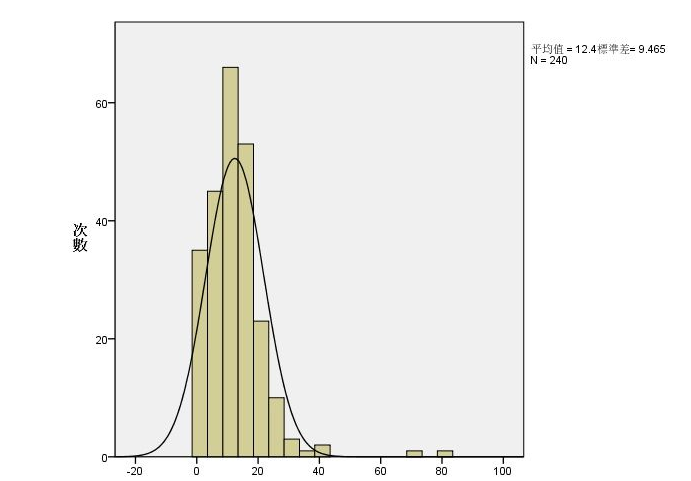
从图中我们可以获取什么?
集中趋势
高峰组段在什么位置
离散趋势
数据分布范围是什么,分散程度如何
分布形状
是否对称,分布曲线的形状
正负偏
分布特征
偏态 峰态
集中趋势
均数(mean)
描述一组数据在数量上的平均水平
总体均数和样本均数的符号
均数的优点:
- 高度浓缩了数据的精华,使大量的观测数据转变成一个代表性的数值。比较敏感,数据任何一个值发生变化,均数都会随之改变。
- 大家熟知、都比较喜欢用、便于比较和传播
均数的缺点:
- 大锅饭:把各个观测数据之间的差异性掩盖了
- 均数受极值的影响很大
中位数(Median)
在均数不好用的时候,我们可以考虑使用中位数
将全体数据从小到大排列,在整个数列中处于中间位置的那个值就是中位数
个数为奇数的中间的那个数字, 个数为偶数中间俩个数字相加除以2
中位数的优点:
不受极端值的影响,在具有个别极大或极小值的分布数列中,中位数比均数更具有代表性
中位数的缺点:
不是所有人都能理解
损失信息:只考虑居中位置,其他变量值比中位数大多少或小多少,它无法反映出来,所以我们也是只能看到部分信息。
中位数的应用场景:对于对称性的数据,优先均数,仅仅对于均数不能使用的情况才使用中位数加以描述。
众数
一组数据当中,出现次数最多的那个数,工作中用的很少
Excel如何使用:均数、中位数、众数
均数:average()
中位数:median()
众数:mode()
离散趋势
提问:如果用平均数来代表样本平均水平的话,对个体而言,什么指标可以代表其离散程度大小
离均差:x-μ
个体偏离均值的程度
提问:可否用离均差的总和来表示整个样本的离散程度
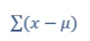
不可以,离均差有正负之分,加和会抵消为0
那怎么办,怎么解决正负号的问题?
可以考虑绝对值
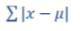
but这种方式不便于计算
该怎么办,怎么找到一种既好算,又能处理正负号的问题?
求离均差的平方和
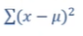
但是如果比较两个样本的离均差,一个样本量是10个,一个是1000个,实际上二者的离散程度是一样的,但是因为数量不同,造成平方和相加和数值差异很大,这该怎么办?
显然,我们发现离均差平方和的大小跟样本量有关
如果我们能够把离均差平方和/样本量,是不是就解决了这个问题
那其实这个就是方差的概念
总体方差公式
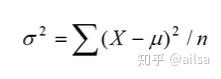
总体标准差=离均差平方和/样本量
方差开根号,是我们日常生活中常用的代表离散程度的指标
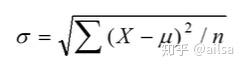
但是在实际的工作中,我们对于总体的数据往往是无法获取的,所以通常是通过随机抽取部分样本数据进行计算,因此公式稍微有点差别
样本标准差
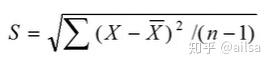
变异系数
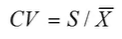
变异系数 = 标准差/均值
变异系数解决了不同样本变异程度对比的问题
常见的四分位数
P25、P50和P75分位数分别称作下四分位数,中位数 上四分位数

Exce实现
方差:var.s(num1,num2,....)
标准差:stdev.s(num1,num2,....)
变异系数:标准差/均值
百分位数:percentile.inc(array,k)
四分位数:quartile.inc(array,k)
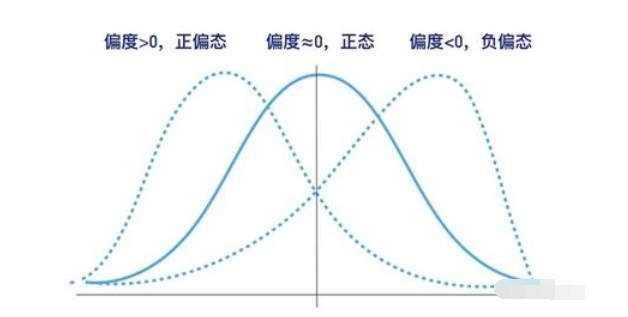
分布形状
针对某种分布进行进一步的特征描述,常见的是用于正态分布的两个指标
- 偏度系数 正态 正偏态 负偏态
- 峰度系数 正态 平阔峰 尖峭峰

Excel实现
偏度:skew()
峰度:kurt()