通过SQL绘制杨辉三角

无意中在csdn上看到一帖有关绘制杨辉三角的sql表达式，感觉很有意思。后来自己想下不借助临时表，根据杨辉三角的组合数计算方法C(n,m)=n!/[m!(n-m)!]，进行绘制。

以下是完整的SQL代码：

use tempdb
go
set nocount on
declare @rows int=10, --行数，根据实际来控制
        @x int=1,@y int=1,@sql nvarchar(max),@cols int
 
/*
根据杨辉三角的组合数计算方法：C(n,m)=n!/[m!(n-m)!]进行绘制
参照：http://baike.baidu.com/view/7804.htm
*/
 
set @cols=@rows*2-1
;with cte_n as
(
    select r from (select row_number() over(order by a.object_id) as r from sys.all_columns a ) x where r<=@rows*2
)
,cte_1 as(select n.r,b.data_lse
            from cte_n n
                cross apply(select 'select '+stuff((select ',rtrim('+isnull(F1.v+'/(('+F2.v+')*'+F3.v+')','''''') +') as '+quotename(isnull(nullif((m.r +(@rows-n.r)+(m.r-1)*1)%@cols,0),@cols))
                                from cte_n m
                                    outer apply(select stuff((select '*'+rtrim(i.r) from cte_n i where i.r<=isnull((nullif(n.r-1,0)),1) for xml path('')),1,1,'') as v
                                        ) F1
                                    outer apply(select stuff((select '*'+rtrim(i.r) from cte_n i where i.r<=isnull((nullif(m.r-1,0)),1) for xml path('')),1,1,'') as v
                                        ) F2
                                    outer apply(select stuff((select '*'+rtrim(i.r) from cte_n i where i.r<=isnull((nullif(n.r-m.r,0)),1) for xml path('')),1,1,'') as v
                                        ) F3
                                where m.r<@rows*2
                                order by isnull(nullif((m.r +(@rows-n.r)+(m.r-1)*1)%@cols,0),@cols) asc
                                for xml path('')                                    
                                ),1,1,'') as data_lse
                            )b
                where n.r <=@rows
            ) 

    select @sql=isnull(@sql+' union all ','')+data_lse from  cte_1
exec(@sql)

（【注】：当前脚本在SQL Server 2012上测试通过）

效果图：

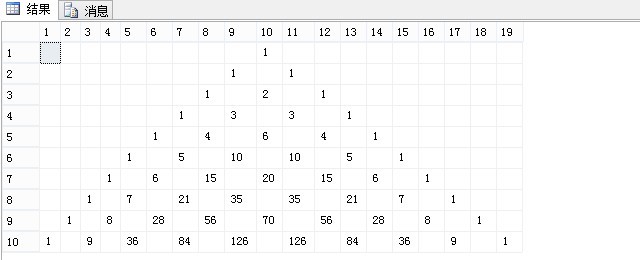
这方法虽然没有借助临时表，也有一个最大的不足就是不能设置太多行，因为在公式（C(n,m)=n!/[m!(n-m)!]）中有n! 和m! 算式，设置行数太多会导致阶乘数据太大，发生数据类型转换溢出。有时间再想办法看能否从表示式中"/"除位置进行优化。