构建乘积数组

给定一个数组A[0,1,...,n-1],请构建一个数组B[0,1,...,n-1],其中B中的元素B[i]=A[0]*A[1]*...*A[i-1]*A[i+1]*...*A[n-1]。不能使用除法。

剑指的思路：

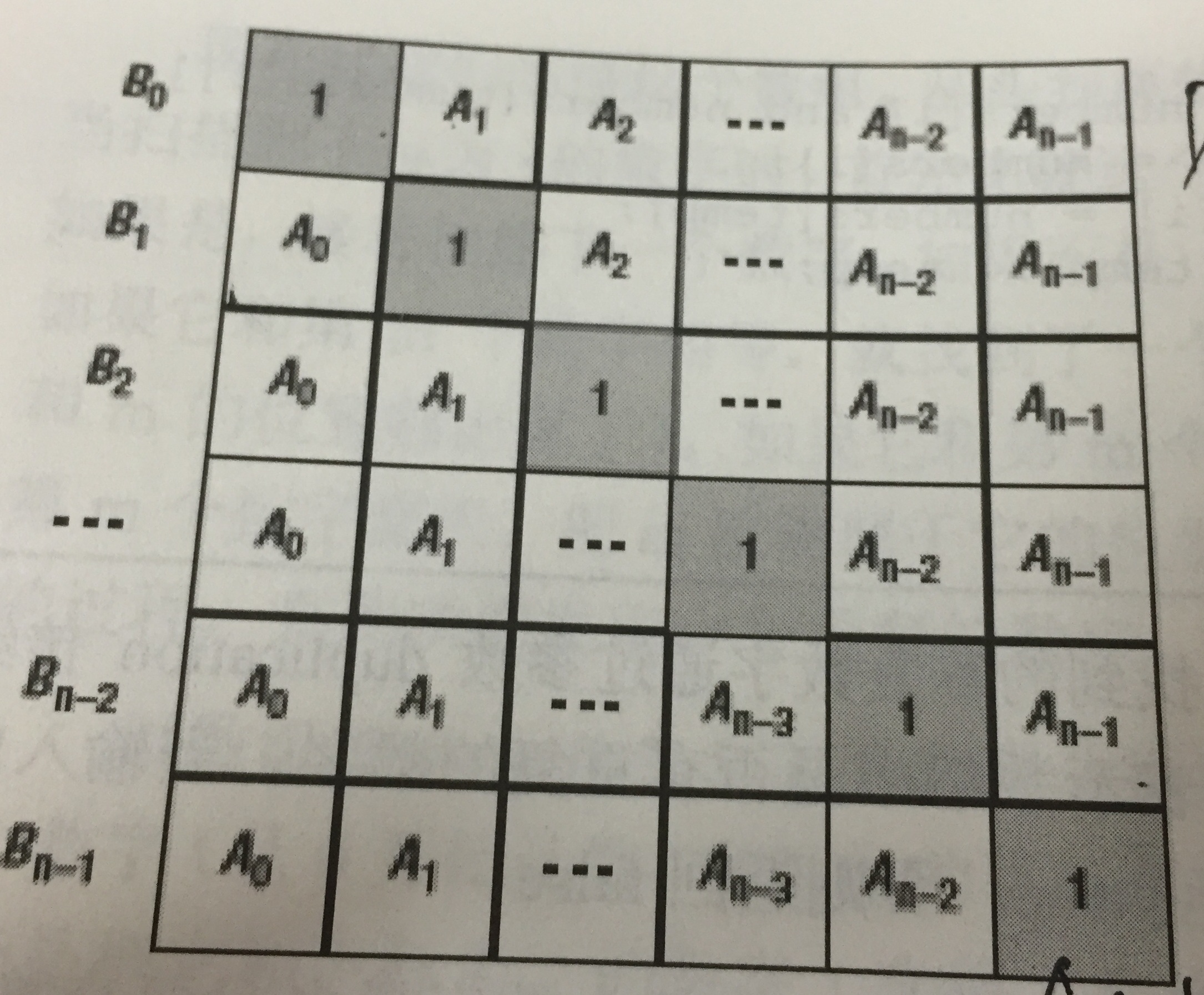
B[i]的值可以看作下图的矩阵中每行的乘积。

  下三角用连乘可以很容求得，上三角，从下向上也是连乘。

  因此我们的思路就很清晰了，先算下三角中的连乘，即我们先算出B[i]中的一部分，然后倒过来按上三角中的分布规律，把另一部分也乘进去。

 

    vector<int> multiply(const vector<int>& A) {
             
        if(A.size()==0) return vector<int>();
        int len=A.size();
        
        vector<int>B(A.size());
        if(len!=0)
        {
            int result=1;
            B[0]=1;//注意此处
            //计算下三角
            for(int i=1;i<len;i++)
            {
                B[i]=B[i-1]*A[i-1];
            }
            result=1;
            //计算上三角
            for(int i=len-2;i>=0;i--)
            {
                result*=A[i+1];
                B[i]*=result;
                
            }
        }
        return B;
    
    }