5.3 删除二叉搜索树的最大元素和最小元素

在5.2中完成了树的遍历，这一节中将对如何从二叉搜索树中删除最大元素和最小元素做介绍：
我们要想删除二分搜索树的最小值和最大值，就需要先找到二分搜索树的最小值和最大值，其实也还是很容易的，因为根据二叉搜索树的特点，它的左子树一定比当前节点要小，所以二叉搜索树的最小值一定是左子树一直往下走，一直走到底。同样在二叉搜索树中，右子树节点值，一定比当前节点要大，所以右子树一直往下走，就一定是最大值。

注意向左走一直到走不动并不是一定要达到叶子节点，只用达到走不动为止，看下图的例子:

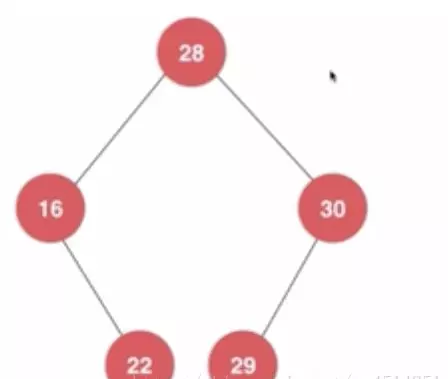
向左走到16就走不动了，但是16下面还有元素。

一、查询操作

1.1 查询二分搜索树的最小节点

 // 寻找二分搜索树的最小元素
    public E minimum() {
        if (size == 0) {
            throw new IllegalArgumentException("BST is empty");
        }

        Node ninNode = minimum(root);
        return ninNode.e;
    }

    // 返回以node为根的二分搜索树的最小值所在的节点
    private Node minimum(Node node) {
        if (node.left == null) {
            return node;
        }

        //返回相应的节点的左子树的最小值
        return minimum(node.left);
    }

1.2 查询二分搜索树的最大节点

 // 寻找二分搜索树的最大元素
    public E maxmum() {
        if (size == 0)
            throw new IllegalArgumentException("BST is empty");
        Node maxNode = maxmum(root);

        return maxNode.e;
    }

    // 返回以node为根的二分搜索树的最大值所在的节点
    private Node maxmum(Node node) {
        if (node.right == null) {
            return node;
        }

        return maxmum(node.right);
    }

二、删除操作

删除最小值的思路：
1）如果要删除的节点是叶子节点，那么直接删除
2）如果要删除的节点下面有右子树，那么只用将其下的右子树整体上移成为上一个节点的左子树即可

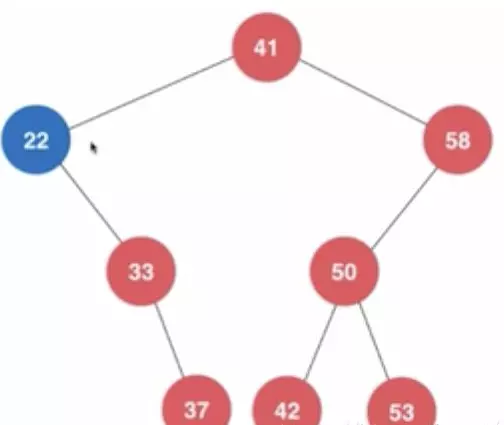
当删除22这个节点后，把33这个节点及其以下的子树变成41节点的左子树即可。

2.1 删除最小值

  public E removeMin() {
        E ret = minimum();//获取最小元素
        root = removeMin(root);

        return ret;
    }

    // 删除掉以node为根的二分搜索树中的最小节点
    // 返回删除节点后新的二分搜索树的根
    private Node removeMin(Node node) {

        // 递归的终止条件，当前节点没有左子树了，那么就是最小节点了
        // 如果是最小节点，我们要做的是删除当前节点，但是当前节点很可能是有右子树的
        // 我们先把该节点的右子树节点保存，然后就删除掉该右子树节点，最后把右子树节点返回即可
        if (node.left == null) {
            Node rightNode = node.right;
            node.right = null; //左节点为空了，让右子树也为空，相当于脱离了树
            size--;
            return rightNode;//返回右子树是为了后面的绑定操作
        }

        // 没有递归到底的情况，那么就递归调用其左子树，这个调用的过程会返回被删除节点的右子树，
        //将返回的右子树重新绑定到上一层的node的左节点上就相当于彻底删除了那个元素
        node.left = removeMin(node.left);

        return node;// 删除后，根节点依然是node，返回即可
    }

2.2 删除最大值

 // 从二分搜索树中删除最大值所在节点
    public E removeMax() {
        E ret = maxmum();
        root = removeMax(root);
        return ret;
    }

    // 删除掉以node为根的二分搜索树中的最大节点
    // 返回删除节点后新的二分搜索树的根
    private Node removeMax(Node node) {
        if (node.right == null) {
            Node leftNode = node.left;
            node.left = null;
            size--;
            return leftNode;
        }

        node.right = removeMax(node.right);//等号"="左边的相当于上一次的right,右边相当于下一次返回的结果
        return node;

    }

源码地址 https://github.com/FelixBin/dataStructure/blob/master/src/BST/BST.java

推荐是最好的支持，关注是最大的鼓励。亲爱的朋友，很荣幸在园子里遇到您。