编程作业1：线性回归
介绍：
在本节练习中，您将实现线性回归并了解它的对数据如何处理。在开始本节编程练习前，我们强烈推荐观看视频讲座并回顾相关的话题。
要开始练习前，您需要下载初始代码并解压到你希望完成联系的目录中去。如果有需要，可以使用octave/matlab中cd命令去更改该目录。您也可以在课程网站的“环境设置说明”中找到安装Octave/Matlab的说明。
本练习中包含的文件：
ex1.m - Octave/MATLAB 脚本指导你完成练习
ex1 multi.m - 练习后面部分的octave/matlab脚本
ex1data1.txt - 一元线性回归数据集
ex1data2.txt – 多元线性回归数据集
submit.m - 将解决方案发送到我们服务器的提交脚本
[*] warmUpExercise.m - octave/matlab中的简单示例函数
[*] plotData.m – 数据显示函数
[*] computeCost.m - 计算线性回归成本的函数
[*] gradientDescent.m – 运行梯度下降函数
[+] computeCostMulti.m – 多元线性回归代价函数
[+] gradientDescentMulti.m – 多元变量梯度下降法
[+] featureNormalize.m – 归一化特征函数
[+] normalEqn.m - 计算法方程的函数
* 指示你要完成的文件
† 表示可选练习
在整个练习中，您将使用脚本ex1.m和ex1 multi.m。这些脚本为问题设置数据集和你将要调用的函数。你只是按照中的说明修改其他文件中的功能这项任务。对于本编程练习，你只需要完成练习的第一部分，即实现一个变量的线性回归。第二部分为可选，包含多变量的线性回归。
哪里能得到帮助
本课程的来呢西使用Octavel1或Matalab非常适合于数值计算的高级语言。如果您没有安装Octave或Matlab，请参阅课程网站“环境设置说明”中的安装说明。在octave/matlab命令行中，键入help并后跟函数名，将显示内置函数的文档。例如，“帮助绘图”将显示用于绘图的帮助信息。更多关于Octave资料说明可以在Octave资料网页找到，更多关于MATLAB资料说明可以在MATLAB资料网页找到。我们也强烈鼓励利用网上讨论与其他学生讨论练习。但是，不要查看其他人编写的任何源代码，也不要与其他人共享您的源代码。
1、 简单的octave/Matlab 函数
。。。
2、一元线性回归
在本节的部分练习中，你将使用一元线性回归去预测快餐车的性能。假设你是一家餐饮连锁店的首席执行官，正在考虑在不同的城市开设新的门店。这家连锁店在各个城市都有快餐车，而且你也有来自各个城市的收入和人口数据。
您希望使用此数据帮助您选择下一个要展开的城市。文件ex1data1.txt包含线性回归问题的数据集。第一列是一个城市的人口，第二列是该城市快餐车的收益。负值代表损失，ex1.m脚本已经设置为为您加载此数据。
2.1 描绘数据
在开始任何任务前，将数据可视化时十分有用的。对于这个数据集，可以使用散点图来可视化数据，因为它只有两个属性可绘制（profit和population）。（你在现实生活中会遇到的许多问题都是多维的不能绘制在二维图上。
2.2 梯度下降法
在这一部分，你将使用梯度下降法求解线性回归的参数theta
2.2.1 更新方程
线性回归的目标是最小化成本函数
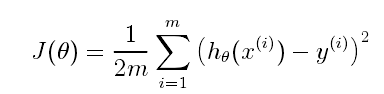
假设hΘ(x)有下列形式给出：
hΘ(x) = ΘTx=Θ0+Θ1x1
回想一下，模型的参数是θj值。你将调整这些值去最小化代价函数J(Θ)。一种算法是批梯度下降法（batch gradient descent algorithm.）。每次迭代都要更新
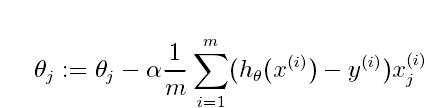（对所有的j，同时更新θj）
每一步梯度下降，你的参数θj都将接近最优值（最低代价成本J(Θ)）。
实现说明：我们将每一个样本数据最为一行存贮在X矩阵中通过Octave/MATLAB。考虑到截距项（θ0），我们在矩阵X添加了额外的一列并且都设置为1。这允许我们把θ0当作另一个“特征”。
2.2.2 实现
在ex1.m中，我们已经建立了线性回归的数据。在下面的几行中，我们在数据中添加另一个维度，以适应θ0截距项。我们初始化参数为0并且·学习效率为0.01。
2.2.3 计算代价函数J(Θ)
当你执行梯度下降学习最小化成本函数J（Θ）时，通过计算成本来监控收敛是有帮助的。在本节中，您将实现一个函数来计算j(Θ)，以便检查梯度下降实现的收敛性。
下一个任务是完成computecost.m文件中的代码，这是一个计算j（θ）的函数。在执行此操作时，请记住变量x和y不是标量值而是矩阵，矩阵的行代表了来自训练集的样本。
一旦你完成了这一函数，下一步就是在ex1.m将会运行computeCost一次（Θ被初始化为0），你将看到代价成本打印到屏幕上你应该预计代价是32.07。
你现在需要提交你的解决方案。
2.2.4 梯度下降法
下一步，您将在完成文件 gradient descent.m实现梯度下降。循环结构已经为您编写好了，您只需要在每次迭代中提供θ的更新。当你编程时候，确保你明白你在试图优化什么和正在更新什么。记住代价函数J（Θ）的参数是Θ，而不是x，y。如果您不确定，请参阅本讲义中的公式和视频讲座。
验证梯度下降是否正常工作的一个好方法是检查J（Θ）是否每一步都在减小。gradientDescent.m 前面部分代码在每一次迭代都调用了computeCost 并且计算了成本。
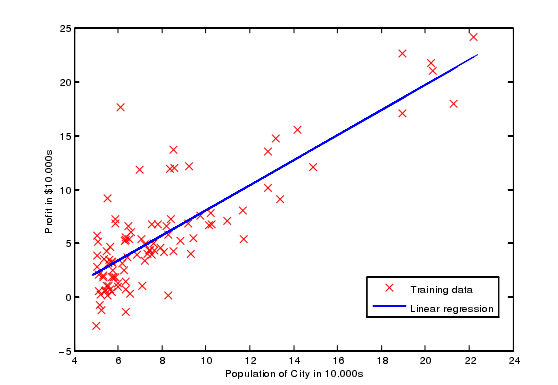
假设你已经正确实现了梯度下降和computecost，j（θ）的值永远不会增加，而且应该在算法结束时收敛到一个稳定值。在你完成后，ex1.m将会用你的参数来线性拟合。
结果应该类似于图2：θ的最终值也将用于预测有35000人和70000人的地区的收益。注意下面几行ex1.m使用矩阵乘法而不是显式求和或循环来计算预测。这是octave/Matlab中矢量化示例代码。
你现在需要提交你的解决方案：
2.3 调试
在实现梯度下降时，请记住一下几点：
- octave/Matlab数组索引从一开始，而不是从零开始。如果将θ0和θ1存储在一个称为θ的向量中，则值为θ（1）或θ（2）。
-
如果在运行时看到许多错误，请检查矩阵运算，以确保添加和乘以兼容维度的矩阵。打印变量的维度（size）将帮助您调试。
2.4 可视化J（Θ）
为了更好地理解成本函数j（θ），现在将在θ0和θ1的二维网格上绘制成本。您不需要为这个部分编写任何新的代码，但是您应该了解已经编写的代码是如何创建这些图像的。在ex1.m的下一步中，将使用您编写的computecost函数代码来计算值集合上的j（θ）
在执行这些行之后，将有一个由j（θ）值组成的二维数组。然后，脚本ex1.m将使用这些值，使用surf和contour命令生成j（θ）的曲面和等高线图。图像应该看起来
如图3所示：
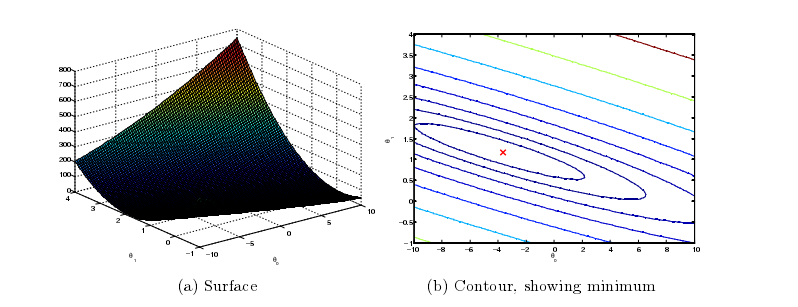
这些图的目的是向您展示j（θ）如何随θ0和θ1的变化而变化。成本函数j（θ）是碗形的，具有全局最小值。（三维曲面图中更容易看到）。这个最小值是θ0和θ1的最佳点，梯度下降的每一步都接近这一点。
可选练习
如果你已经成功地完成了上述材料，恭喜！你现在了解线性回归，应该能够开始在拥有自己的数据集。对于本次编程练习的其余部分，我们已经包括了以下内容可选练习。这些练习将有助于你加深理解。如果你能做到这一点，我们也鼓励你完成。
3.多元线性回归
在这一部分中，您将使用多个变量实现线性回归来预测房价。假设你卖掉房子想知道一个好的市场价格是多少。一种方法是首先收集最近出售房屋的信息，并制定房屋价格模型。文件ex1data2.txt包含俄勒冈州波特兰市房价的训练集。第一列是房子的大小（平方英尺），第二列是卧室的数量，第三栏是价格。ex1 multi.m脚本已建立以帮助您逐步完成此练习。
3.1特征归一化
ex1 multi.m脚本将从加载和显示一些来自这个数据集的值。通过查看这些值，注意房屋大小卧室的数量是房间的1000倍。当特征差别成数量级时，首先执行特征缩放可以使梯度下降收敛更快。
您的任务是完成在featureNormalize.m中的代码：
•从数据集中减去每个特征的平均值。
•减去平均值后，除以各特征值的方差。
标准差是一种测量特定特征值范围内变化大小的方法（大多数数据点位于平均值的±2个标准差范围内）；获取最大最小值是另外一种方法。在Octave/Matlab中，可以使用“std”函数计算标准差。
例如， 在featureNormalize.m中。X（：，1）包含训练集中x1（房屋大小）的所有值，因此std（x（：，1）计算房屋大小的标准偏差。在调用 featureNormalize.m时，对应于X0＝1的1的额外列尚未被添加到X。（详细细节参考ex1 multi.m）。您将对所有特性执行此操作，并且您的代码应该使用所有大小的数据集（任何数量的特性/示例）。注意每个矩阵x的列对应于一个特征。
你现在应该提交你的解决方案
注意事项：当规范化特征时，重要的是存储用于标准化的值-用于计算的平均值和标准偏差。在从模型中学习参数之后，我们经常想要预测我们以前没有见过的房子的价格。给定一个新的X值（客厅面积和卧室数），我们必须使用我们之前从训练中计算出来的平均值和标准差来标准化X。
3.2 梯度下降
前面我们实现了一元变量线性回归的梯度下降法，唯一不同点是在矩阵X对了一个特征。假设函数和批量梯度下降更新规则保持不变。您应该在computecostmulti.m和gradientdescentmulti.m中完成代码实现多元线性回归的成本函数和梯度下降。如果前一部分（单变量）中的代码已经支持多个变量，也可以在这里使用。请确保您的代码支持任意数量的功能，并且已经很好地矢量化了。你可以使用‘size(X, 2)’ 去查看当前数据集有多少特征。
你应该提交你的方案：
实施说明：在多变量的情况下，成本函数也可以用以下形式写成：
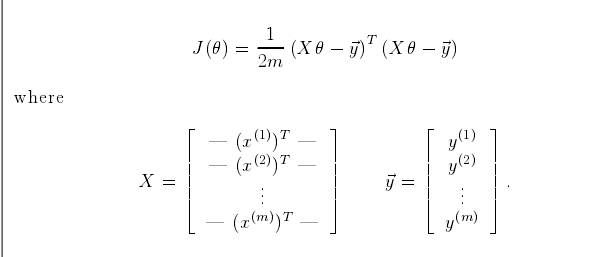
当使用像Octave/Matlab之类的数值计算工具时，矢量化版本是非常重要的。如果你很擅长矩阵运算，你可以证明自己，这两种形式是等价的。
3.2.1选择性（未分级）练习：选择学习率
在这部分练习中，你将尝试不同的学习率和找出一个快速收敛的学习率。你可以修改ex1.m中设置学习率部分来修改学习率。在选择的学习率下，ex1 multi.m调用gradientDescent.m中的函数执行50次迭代。该函数还应返回向量J中J（θ）的历史值。在最后一次迭代之后，ex1 multi.m脚本根据迭代次数绘制J（Θ）值。如果你在一个好的范围内选择一个学习率，你的图像看起来类似于图4。如果你的图看起来很不一样，特别是如果你的j（θ）值增加甚至增加，调整你的学习速度，再试一次。我们建议在对数刻度上尝试学习速率α的值，乘以约为先前值的3倍（即0.3、0.1、0.03、0.01等）。您还可能希望调整运行的迭代次数，这样可以帮助您了解曲线的整体趋势。
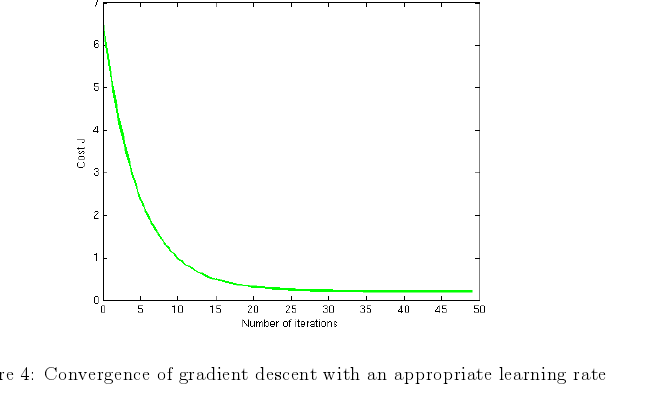
实现注意：如果你的学习速率太大，J（Θ）会发散和“炸掉”，导致计算机计算的数值太大。在这些情况下，octave/matlab将倾向于返回nans。nan代表“非数字”，通常是由undefined引起的包括－∞和＋∞的操作。
Octave/MATLAB 技巧：为了比较不同的学习率对收敛的影响，将不同学习率的J绘制在同一种图上很有用。在Octave/Matlab中，在多元线性回归时可以通过执行‘hold on’ 命令在不同的 plots之间。具体地说，如果你尝试了三个不同的alpha值（你应该尝试更多的值），并且把成本存储在J1、J2和J3，您可以使用以下命令将它们绘制在同一个图形上
注意随着学习速率的变化，收敛曲线的变化。学习率很低，你应该知道梯度下降需要长时间收敛到最优值。相反，有一个大的学习速率，梯度下降可能不收敛，甚至可能发散！使用找到的最佳学习速率，运行ex1 multi.m脚本实现梯度下降，直到找到最后的Θ。下一步，用这个θ值来预测1650平方英尺的房屋价格3间卧室。稍后将使用正常方程的实现检查你的预测。当你完成时，别忘了标准化你的特征。
您不需要提交这些可选（未分级）的任何解决方案练习。
3.3正态方程
在讲座视频中，你了解到线性回归的封闭形式解决方案是
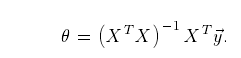
使用此公式不需要任何特征缩放，您将在一次计算中得到精确的解决方案：不存在类似于在梯度下降中多次循环直到收敛。
完成normaleqn.m中的代码，使用上面的公式计算θ。请记住，虽然您不需要缩放功能，但我们仍然需要在x矩阵中添加一列1，以获得一个截距项（θ0）。
ex1.m中的代码将为您添加1到x的列。
现在你需要提交你的方案：
可选（未分级）练习：现在，一旦你用这个找到θ方法，用它对一个1650平方英尺的3间卧室。你应该给出与价值相同的预测价格。使用具有梯度下降的模型（见第3.2.1节）