一、遗传算法原理介绍
遗传算法(Genetic Algorithm)是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法。遗传算法是从代表问题可能潜在的解集的一个种群(population)开始的,而一个种群则由经过基因(gene)编码的一定数目的个体(individual)组成。每个个体实际上是染色体(chromosome)带有特征的实体。染色体作为遗传物质的主要载体,即多个基因的集合,其内部表现(即基因型)是某种基因组合,它决定了个体的形状的外部表现,如黑头发的特征是由染色体中控制这一特征的某种基因组合决定的。因此,在一开始需要实现从表现型到基因型的映射即编码工作。由于仿照基因编码的工作很复杂,我们往往进行简化,如二进制编码,初代种群产生之后,按照适者生存和优胜劣汰的原理,逐代(generation)演化产生出越来越好的近似解,在每一代,根据问题域中个体的适应度(fitness)大小选择(selection)个体,并借助于自然遗传学的遗传算子(genetic operators)进行组合交叉(crossover)和变异(mutation),产生出代表新的解集的种群。这个过程将导致种群像自然进化一样的后生代种群比前代更加适应于环境,末代种群中的最优个体经过解码(decoding),可以作为问题近似最优解。[1]
简单而言,遗传算法是一种模拟自然界生物进化过程,通过不断试错和筛选得到最优解的算法。
二、遗传算法的计算机表达
在对遗传算法的流程进行介绍前,本节将以字符编码方式为例对如何以计算机语言表达种群、个体等生物概念进行介绍。
2.1 个体、染色体、基因
个体是由染色体组成的带有特定属性的实体,一般而言,为了简化概念,我们认为一个个体由一条染色体组成,两者相互等价。因此,在后文中个体与染色体统一称为染色体。
由生物知识可知,染色体由一个个独立的基因组成,为了在计算机中表达这一概念,我们建立一维数组代表染色体,数组内每一个元素代表一个基因。如图2.1所示:

图2.1 染色体的计算机表达(字符编码)
图2.1左侧为A、B、C三条独立的染色体,其内部的字符代表其所在位置的基因。在此,我们采用一种伪16进制的字符编码方式对基因进行表达。字符取值范围为1~10、A~F共16个值,A~F分别表示11~16。
注:此处并非真正的16进制,仅是一种为了表达两位数以上基因且便于理解而设置的伪16进制表示方法。之所以不使用整形变量数组,习惯使然。
图2.1右侧为染色体的计算机表达,按照从左到右的次序,其基因作为元素被储存在数组中。一般来说,为了便于计算和存储,我们认为所有染色体的长度都相同,在程序中可以声明一个全局常量lengthOfChromosome用以表达。
2.2 种群

图2.2 种群的计算机表达(字符编码)
由第一节给出的定义可知,种群是个体的集合,因此,相对于使用一维数组表达的染色体,我们使用二维数组表达由多个染色体组成的种群,如图2.2右侧。行号代表染色体编号,列号代表染色体内基因编号。
注:2.1中假定染色体长度固定的作用便体现在此,由于染色体长度固定,我们很容易就可以建立起由二维数组表达的种群。
2.3 变异——基因重组、基因突变
在生物概念中,变异包括基因重组、基因突变、染色体变异在内。由于基因突变与染色体变异作用类似,为了简化算法,仅选取基因重组、基因突变两种进行表达。首先,对基因重组与基因突变的意义做出解释。
基因突变:基因突变是生物变异的根本来源,为生物的进化提供了原材料。[2]
基因重组:基因重组可以产生多种多样的基因组合的子代,其中有一些子代会含有适应某种环境变化的基因组合。所以说,基因重组是生物变异的来源之一,是形成生物多样性的重要原因,对生物的进化具有重要的意义。[2]
简单地说,基因突变保证种群能够出现新的基因型,是进化的根本保障;而基因重组为提高种群内生物多样性提供了条件,为种群的进化提供了足够多的试错样本。
2.3.1 基因重组——单点互换、基因移位(并非严谨称呼,请勿与生物学术概念等同)
2.3.1.1 单点互换
单点互换即在染色体中选择任意两个不同位置的基因进行交换,达到互换位置的目的。示意图如下:
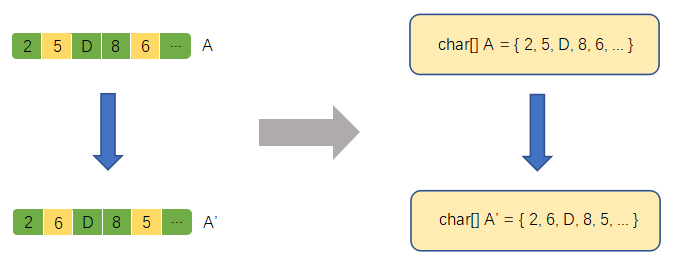
图2.3.1.1 单点互换的计算机表达(字符编码)
由上图可以看出,A染色体左数第二个基因与左数第五个基因发生单点交换得到染色体A'。在算法中则体现为,字符数组A第二个元素与第五个元素的值发生交换。
2.3.1.2 基因移位
显而易见,一次单点换位最多只改变两个基因的位置,这给染色体带来的变化并不大。当我们要求每次变异染色体都能发生足够大的变化,该怎么做呢?这时,可以使用基因移位的办法。仍以染色体A为例,如图所示:
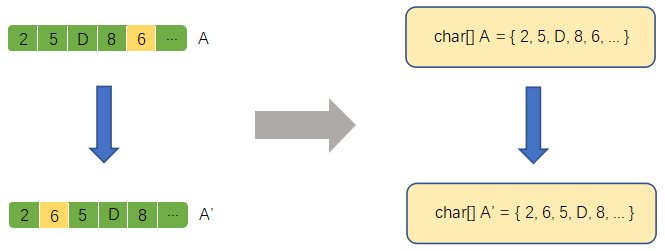
图2.3.1.2 基因移位的计算机表达(字符编码)
如上图所示,我们随机选取染色体A内任意基因,并将其插入到原染色体除基因初始位置以外的任意位置。通过这种方式,我们能够给染色体带来基因序列的较大变化。
注:根据应用场景和规则限制的不同,参与基因移位的基因数可以是多个,例如染色体A中8、6两个基因同时插入到染色体其他位置。不过,在特定情况下,基因移位给染色体基因序列带来的变化与单点互换接近,这将在4.1应用实例中进行解释。
2.3.2 基因突变

图2.3.2 基因突变的计算机表达(字符编码)
在生物概念中,基因突变式发生在基因层面的改变,会产生一个新的基因,这正是自然种群变异的根本来源。在遗传算法中,由于基因往往具备特定的意义(任务、判断选择等),我们不可能产生一个不存在于既定基因取值范围(1~F)外的基因。因此,在遗传算法中,基因突变仅产生既定取值范围内的基因。如上图,基因8由于基因突变变成基因1,反映在计算机中则体现为元素值的改变。
2.4 适应度fitness
适应度(fitness)即在特定评价标准下各种群的指标值,在不同应用环境下结果不同。在此仅简述定义,4.1应用实例将给出一个实例。
2.5 选择——轮盘赌法
为了模拟自然界“物竞天择,适者生存”的选择过程,我们选择轮盘赌法进行模拟。
轮盘赌法的实质是一种基于概率的选择算法,参与选择的个体被选中的概率与其适应度正相关。设染色体A、B、C的适应度分别为6、3、13,得到轮盘如下图所示。
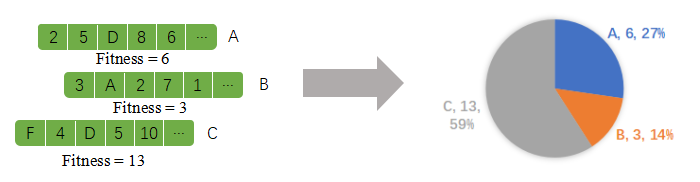
图2.5-1 轮盘示意图
在得到轮盘概率分布后,我们可以通过概率累加建立一条取值范围为[0,1)的线段。如下图:
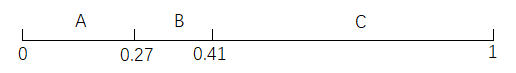
图2.5-2 概率累加直线示意图
在算法中,我们可以通过随机生成一个0~1的随机数,若随机数为0.15,则落在[0,0.27)区域,这表示染色体A被选择出来。由于被选取概率与染色体适应度成正比,在统计规律上,适应度高的个体具有更高的可能性被选择出来,从而达到优胜劣汰的目的。
2.6 改进的选择方式——精英染色体
在遗传算法的实际应用中,由于轮盘赌法的随机性较大,种群进化的速度并不快。为了提高种群进化的速度,我们通过人为保留适应度较高的染色体的方式加速这一过程,这些被留下的染色体被称为精英染色体。示意图如下:
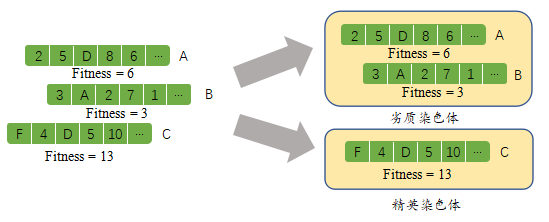
图2.6 精英染色体示意图
假设父代种群包含A、B、C三条染色体,在筛选出精英染色体C后,原种群发生变异,得到新的种群A'、B'、C',新的种群经过轮盘赌筛选得到两个新染色体,与精英染色体C组成子代种群。通过这种方法,能够确保每一代种群最优秀的染色体得以保留,从而提高种群进化速度。
三、遗传算法流程介绍
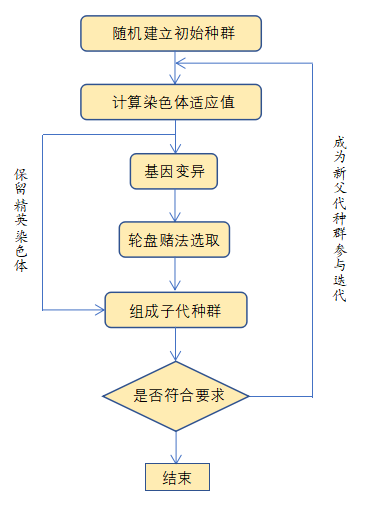
图3 遗传算法流程图
四、应用实例
待补充
参考文献:
[1] 遗传算法,百度百科
[2] 生物(必修二),人教版