数据结构

数据结构

数据结构是指相互之间存在着一种或多种关系的数据元素的集合和该集合中数据元素之间的关系组成。

简单来说，数据结构就是设计数据以何种方式组织并存储在计算机中。

比如：列表、集合与字典等都是一种数据结构。

N.Wirth:“程序=数据结构+算法”

数据结构的分类

数据结构按照其逻辑结构可分为线性结构、树结构、图结构

线性结构：数据结构中的元素存在一对一的相互关系

树结构：数据结构中的元素存在一对多的相互关系

图结构：数据结构中的元素存在多对多的相互关系

列表，顺序表

列表/数组

列表（其他语言称数组）是一种基本数据类型。

关于列表的问题：

列表中的元素是如何存储的？

数组

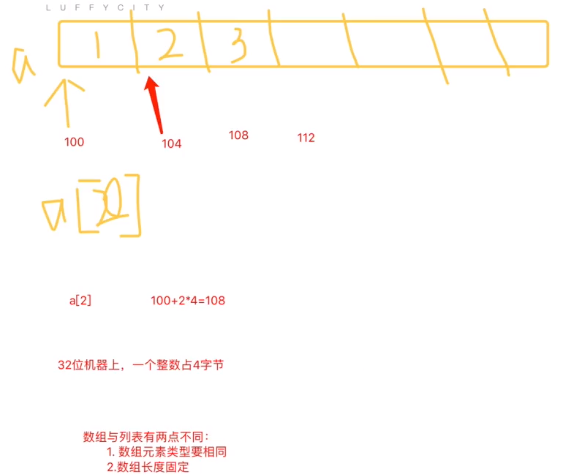
a[2] 100+2*4=108

32位机器上，一个整数占4字节  一个地址占4个字节

数组与列表有两点不同：

1.数组元素类型要相同

2.数组长度固定

列表

列表里存的是，数据的内存地址

删除时【后面的内存地址往前移到删除的位置】，插入，复杂度都是On

列表的基本操作：按下标查找、插入元素、删除元素……

这些操作的时间复杂度是多少？

扩展：Python的列表是如何实现的？

栈

栈（Stack）是一个数据集合，可以理解为只能在一端进行插入或删除操作的列表。

栈的特点：后进先出LIFO（last-in，first-out）

栈的概念：栈顶、栈底

栈的基本操作：

进栈（压栈）：push

出栈：pop

取栈顶：gettop

栈的实现

使用一般的列表结构即可实现栈

进栈：li.append

出栈：li.pop

取栈顶：l[-1]

栈的应用：括号匹配问题

来的跟栈里面的最右边元素匹配，成功则退出【一起出栈】，不匹配报错，栈里的不动，

队列

从列（Queue）是一个数据集合，仅允许在列表的一端进行插入，另一端进行删除。

进行插入的一端称为队尾（rear），插入动作称为进队或入队

进行删除的一端称为队头（front），删除动作称为出队

从列的性质：先进先出（First-in，First-out）

a.直接pop删除第一个，后面都要往前移动，这种方式，复杂度On，不推荐

b.每出栈，就向后移动front指针，存在 front=rear 的情况(d)，导致浪费空间

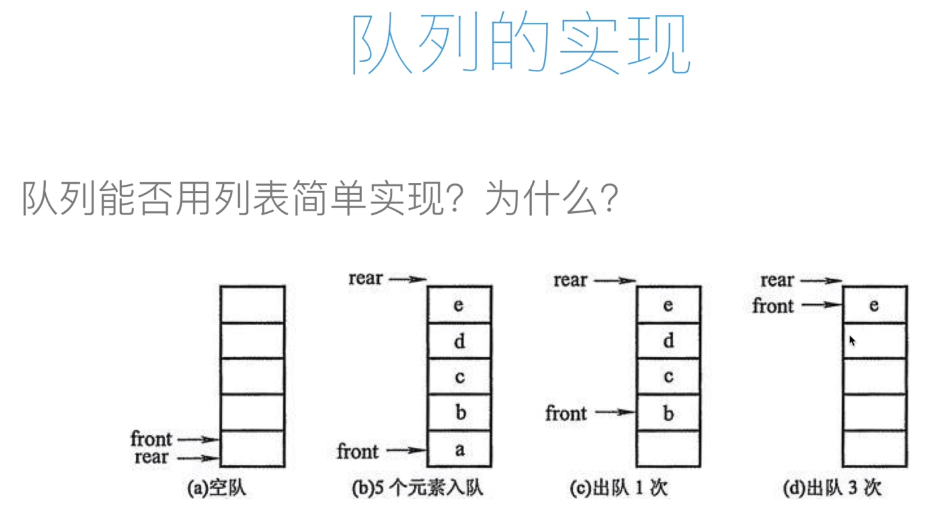
故不能用简单的单向列表实现

c.环形列表

rear = front 规定为空队列

rear = rear + 1 % 12

底层队列的实现

Python 底层在队满时，帮我们实现了，扩充

双向队列

---

栈和队列的应用——迷宫问题

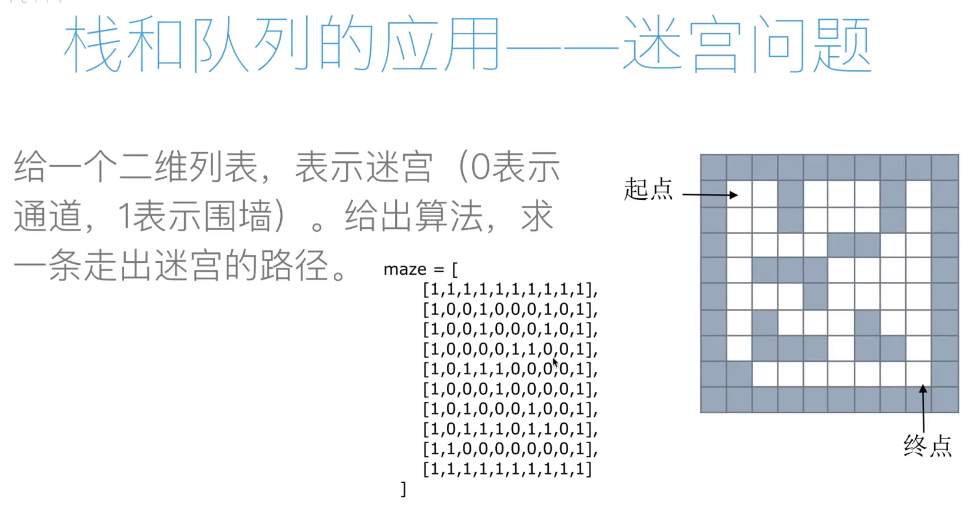
按 上下左右顺序找，无路可走就挨个回退再按顺序找路，看别的能不能走

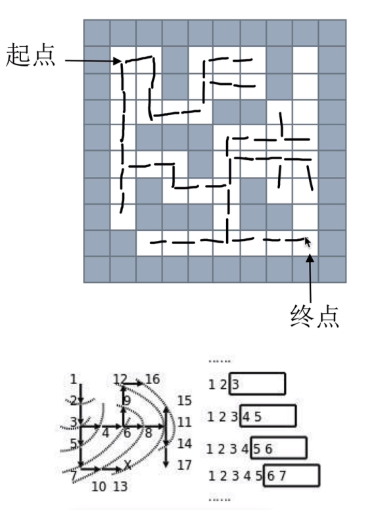
队列里存的是当前走的点

用一个列表存来的路径，方便找到终点后回退

哪个点让他来的

使用队列进行迷宫问题：实现

#! /usr/bin/env python
# -*- coding: utf-8 -*-
# Date: 24/12/2017

from collections import deque

maze = [
    [1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
    [1, 0, 0, 1, 0, 0, 0, 1, 0, 1],
    [1, 0, 0, 1, 0, 0, 0, 1, 0, 1],
    [1, 0, 0, 0, 0, 1, 1, 0, 0, 1],
    [1, 0, 1, 1, 1, 0, 0, 0, 0, 1],
    [1, 0, 0, 0, 1, 0, 0, 0, 0, 1],
    [1, 0, 1, 0, 0, 0, 1, 0, 0, 1],
    [1, 0, 1, 1, 1, 0, 1, 1, 0, 1],
    [1, 1, 0, 0, 0, 0, 0, 0, 0, 1],
    [1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
]

dirs = [
    lambda x, y: (x + 1, y),
    lambda x, y: (x - 1, y),
    lambda x, y: (x, y - 1),
    lambda x, y: (x, y + 1)
]


def print_r(path):
    real_path = []
    i = len(path) - 1
    while i >= 0:  # 第0个元素也要算
        real_path.append(path[i][0:2])  #
        i = path[i][2]  # 带他来的点在path列表中放的位置
    real_path.reverse()  # 倒着回去的，反着输出
    for node in real_path:
        print(node)


def maze_path_queue(x1, y1, x2, y2):
    queue = deque()
    queue.append((x1, y1, -1))  # 起点是由-1带他来的
    path = []
    while len(queue) > 0:
        curNode = queue.pop()
        path.append(curNode)  # 记录当前点
        if curNode[0] == x2 and curNode[1] == y2:
            # 终点
            print_r(path)  # 从path 里面取出路径
            # print(path)
            return True
        for dir in dirs:
            nextNode = dir(curNode[0], curNode[1])
            if maze[nextNode[0]][nextNode[1]] == 0:
                queue.append((nextNode[0], nextNode[1], len(path) - 1))  # 后续节点进队，记录哪个节点带他来的
                # -                                    从哪个来的点在path中的下标
                maze[nextNode[0]][nextNode[1]] = 2  # 标记为已经走过
    else:
        print("没有路")
        return False
maze_path_queue(1, 1, 8, 8)
# path 存储的是出队的点maze