1220. Count Vowels Permutation

Given an integer n, your task is to count how many strings of length n can be formed under the following rules:

• Each character is a lower case vowel ('a', 'e', 'i', 'o', 'u')
• Each vowel 'a' may only be followed by an 'e'.
• Each vowel 'e' may only be followed by an 'a' or an 'i'.
• Each vowel 'i' may not be followed by another 'i'.
• Each vowel 'o' may only be followed by an 'i' or a 'u'.
• Each vowel 'u' may only be followed by an 'a'.

Since the answer may be too large, return it modulo 10^9 + 7.

Example 1:

Input: n = 1
Output: 5
Explanation: All possible strings are: "a", "e", "i" , "o" and "u".

Example 2:

Input: n = 2
Output: 10
Explanation: All possible strings are: "ae", "ea", "ei", "ia", "ie", "io", "iu", "oi", "ou" and "ua".

Example 3: 

Input: n = 5
Output: 68

Constraints:

• 1 <= n <= 2 * 10^4

class Solution {
    public int countVowelPermutation(int n) {
        long acount = 1, ecount = 1, icount = 1, ocount = 1, ucount = 1;
        int mod = 1000000007;
        for(int i = 1; i < n; i++) {
            long newac = (ecount + icount + ucount) % mod;
            long newec = (acount + icount) % mod;
            long newic = (ecount + ocount) % mod;
            long newoc = (icount) % mod;
            long newuc = (icount + ocount) % mod;
            
            acount = newac;
            ecount = newec;
            icount = newic;
            ocount = newoc;
            ucount = newuc;
        }
        return (int) ((acount + ecount + icount + ocount + ucount) % mod);
    }
}

hard??

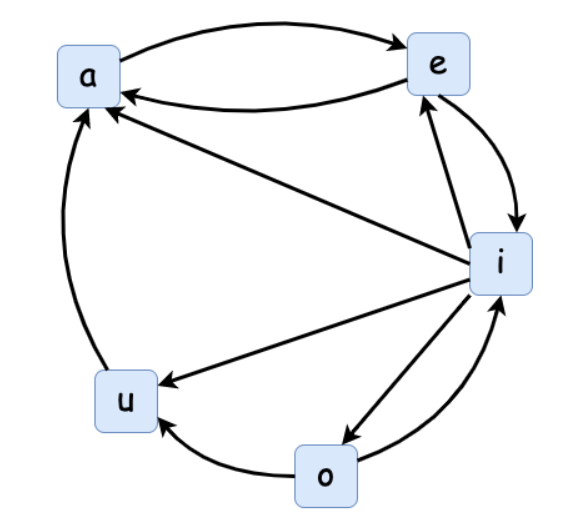
 dp, 对应的是以这个字母为结束的这么多位数的个数