Given two strings str1 and str2, return the shortest string that has both str1 and str2 as subsequences. If multiple answers exist, you may return any of them.
(A string S is a subsequence of string T if deleting some number of characters from T (possibly 0, and the characters are chosen anywhere from T) results in the string S.)
Example 1:
Input: str1 = "abac", str2 = "cab"
Output: "cabac"
Explanation:
str1 = "abac" is a subsequence of "cabac" because we can delete the first "c".
str2 = "cab" is a subsequence of "cabac" because we can delete the last "ac".
The answer provided is the shortest such string that satisfies these properties.
Note:
1 <= str1.length, str2.length <= 1000str1andstr2consist of lowercase English letters.
class Solution { public String shortestCommonSupersequence(String s1, String s2) { int l1 = s1.length(), l2 = s2.length(); int[][] dp = new int[l1 + 1][l2 + 1]; for(int i = 1; i <= l1; i++) { for(int j = 1; j <= l2; j++) { if(s1.charAt(i - 1) == s2.charAt(j - 1)) dp[i][j] = dp[i - 1][j - 1] + 1; else { dp[i][j] = Math.max(dp[i][j - 1], dp[i - 1][j]); } } } StringBuilder sb = new StringBuilder(); while(l1 != 0 || l2 != 0) { if(l1 == 0) sb.insert(0, s2.charAt(--l2)); else if(l2 == 0) sb.insert(0, s1.charAt(--l1)); else if(s1.charAt(l1 - 1) == s2.charAt(l2 - 1)) { sb.insert(0, s1.charAt(--l1)); --l2; } else if(dp[l1][l2] == dp[l1 - 1][l2]) { sb.insert(0, s1.charAt(--l1)); } else if(dp[l1][l2] == dp[l1][l2 - 1]) { sb.insert(0, s2.charAt(--l2)); } } return sb.toString(); } }
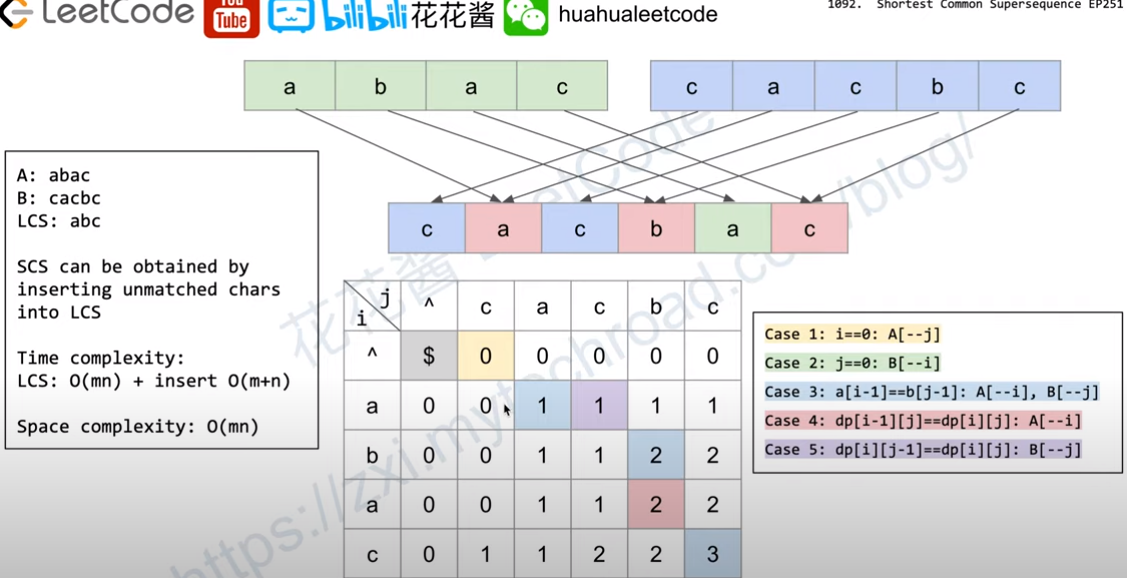
这题有意思啊,从largest common subsequence往前推
先把LCS的dp数组算出来,再通过判断来构造shortes common supersequence,
l1, l2是dp数组的index
具体的判断条件有:
1.l1 == 0, 说明l1已经添加完了,剩下的都是l2的,往里添加即可。注意因为dp数组是l1+1 * l2 + 1, 所以添加的时候要先 -- l2
2.l2 == 0, 说明l2已经添加完了,剩下的都是l1的,往里添加即可。注意因为dp数组是l1+1 * l2 + 1, 所以添加的时候要先 -- l1
下面用i j 代替了
3. s1.charAt(i - 1) == s2.charAt(j - 1), 把这个char insert进去,i--, j--
两个char不相等,那就看一下dp数组跳过了哪个char,把它insert进去
4. dp[i - 1][j] == dp[i][j], 说明是从上面过来的,跳过了s1.charAt(i - 1), 把它insert进去
5.dp[i][j - 1] == dp[i][j], 说明是从左边面过来的,跳过了s2.charAt(j - 1), 把它insert进去
最后返回
https://www.youtube.com/watch?v=rfV2BJp8YA8
花哥救我狗命