1368. Minimum Cost to Make at Least One Valid Path in a Grid

Given a m x n grid. Each cell of the grid has a sign pointing to the next cell you should visit if you are currently in this cell. The sign of grid[i][j] can be:

• 1 which means go to the cell to the right. (i.e go from grid[i][j] to grid[i][j + 1])
• 2 which means go to the cell to the left. (i.e go from grid[i][j] to grid[i][j - 1])
• 3 which means go to the lower cell. (i.e go from grid[i][j] to grid[i + 1][j])
• 4 which means go to the upper cell. (i.e go from grid[i][j] to grid[i - 1][j])

Notice that there could be some invalid signs on the cells of the grid which points outside the grid.

You will initially start at the upper left cell (0,0). A valid path in the grid is a path which starts from the upper left cell (0,0) and ends at the bottom-right cell (m - 1, n - 1) following the signs on the grid. The valid path doesn't have to be the shortest.

You can modify the sign on a cell with cost = 1. You can modify the sign on a cell one time only.

Return the minimum cost to make the grid have at least one valid path.

Example 1:

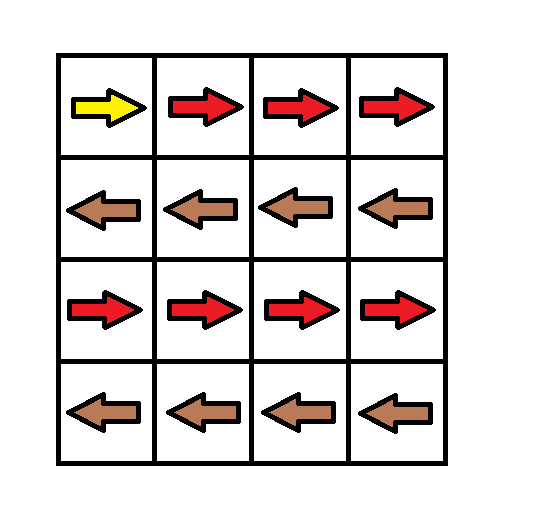
Input: grid = [[1,1,1,1],[2,2,2,2],[1,1,1,1],[2,2,2,2]]
Output: 3
Explanation: You will start at point (0, 0).
The path to (3, 3) is as follows. (0, 0) --> (0, 1) --> (0, 2) --> (0, 3) change the arrow to down with cost = 1 --> (1, 3) --> (1, 2) --> (1, 1) --> (1, 0) change the arrow to down with cost = 1 --> (2, 0) --> (2, 1) --> (2, 2) --> (2, 3) change the arrow to down with cost = 1 --> (3, 3)
The total cost = 3.

Example 2:

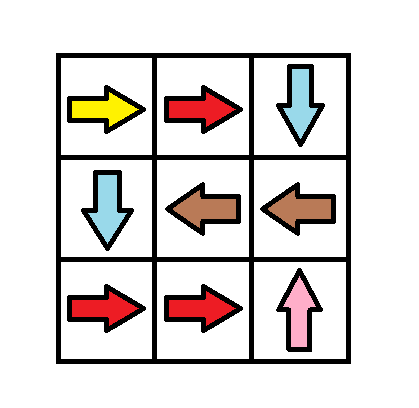
Input: grid = [[1,1,3],[3,2,2],[1,1,4]]
Output: 0
Explanation: You can follow the path from (0, 0) to (2, 2).

Example 3:

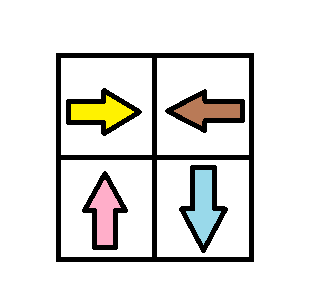
Input: grid = [[1,2],[4,3]]
Output: 1

Example 4:

Input: grid = [[2,2,2],[2,2,2]]
Output: 3

Example 5:

Input: grid = [[4]]
Output: 0

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 100

class Solution {
    int[][] DIR = new int[][]{{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
    public int minCost(int[][] grid) {
        int m = grid.length, n = grid[0].length, cost = 0;
        int[][] dp = new int[m][n];
        for (int i = 0; i < m; i++) Arrays.fill(dp[i], Integer.MAX_VALUE);
        Queue<int[]> bfs = new LinkedList<>();
        dfs(grid, 0, 0, dp, cost, bfs);
        while (!bfs.isEmpty()) {
            cost++;
            for (int size = bfs.size(); size > 0; size--) {
                int[] top = bfs.poll();
                int r = top[0], c = top[1];
                for (int i = 0; i < 4; i++) dfs(grid, r + DIR[i][0], c + DIR[i][1], dp, cost, bfs);
            }
        }
        return dp[m - 1][n - 1];
    }

    void dfs(int[][] grid, int r, int c, int[][] dp, int cost, Queue<int[]> bfs) {
        int m = grid.length, n = grid[0].length;
        if (r < 0 || r >= m || c < 0 || c >= n || dp[r][c] != Integer.MAX_VALUE) return;
        dp[r][c] = cost;
        bfs.offer(new int[]{r, c}); // add to try to change direction later
        int nextDir = grid[r][c] - 1;
        dfs(grid, r + DIR[nextDir][0], c + DIR[nextDir][1], dp, cost, bfs);
    }
}

https://leetcode.com/problems/minimum-cost-to-make-at-least-one-valid-path-in-a-grid/discuss/524886/JavaC%2B%2BPython-BFS-and-DFS

https://leetcode.com/problems/minimum-cost-to-make-at-least-one-valid-path-in-a-grid/discuss/524820/Java-2-different-solutions-Clean-code