1359. Count All Valid Pickup and Delivery Options

Given n orders, each order consist in pickup and delivery services. 

Count all valid pickup/delivery possible sequences such that delivery(i) is always after of pickup(i). 

Since the answer may be too large, return it modulo 10^9 + 7.

Example 1:

Input: n = 1
Output: 1
Explanation: Unique order (P1, D1), Delivery 1 always is after of Pickup 1.

Example 2:

Input: n = 2
Output: 6
Explanation: All possible orders: 
(P1,P2,D1,D2), (P1,P2,D2,D1), (P1,D1,P2,D2), (P2,P1,D1,D2), (P2,P1,D2,D1) and (P2,D2,P1,D1).
This is an invalid order (P1,D2,P2,D1) because Pickup 2 is after of Delivery 2.

Example 3:

Input: n = 3
Output: 90

Constraints:

• 1 <= n <= 500

class Solution {
    public int countOrders(int n) {
        long res = 1, mod = (long)1e9 + 7;
        for (int i = 1; i <= n; ++i)
            res = res * (i * 2 - 1) * i % mod;
        return (int)res;
    }
}

 https://leetcode.com/problems/count-all-valid-pickup-and-delivery-options/discuss/516968/JavaC%2B%2BPython-Easy-and-Concise

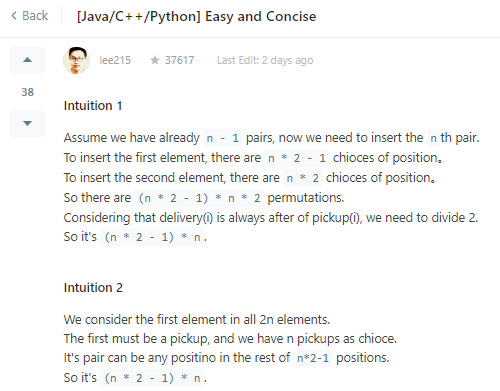
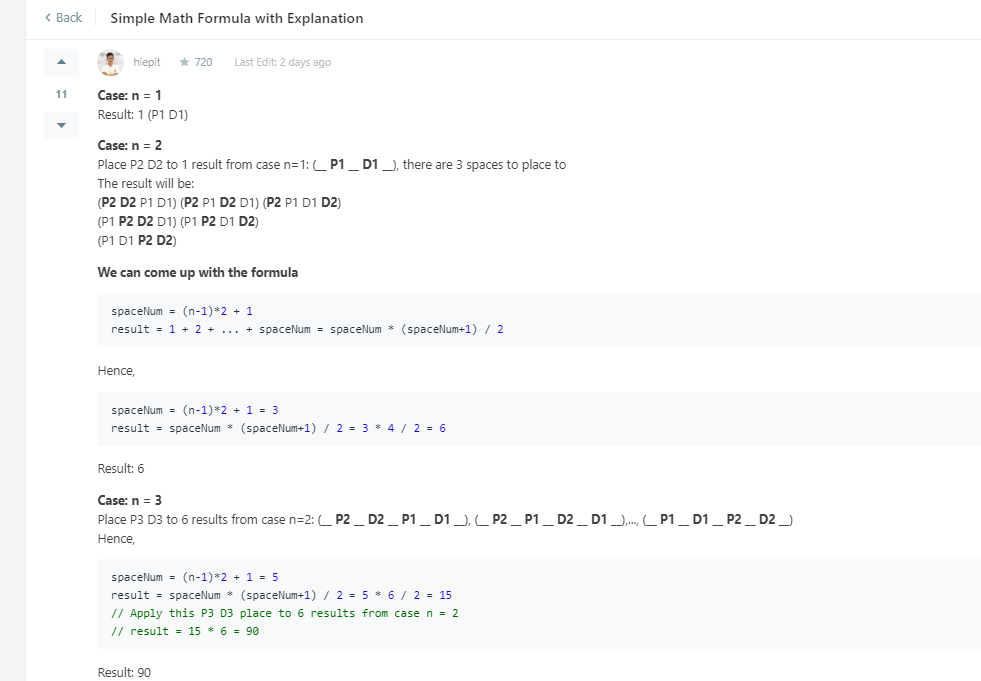
class Solution {
    public int countOrders(int n) {
        long MODULO = (long) (1e9 + 7);
        long ans = 1;
        for (int i = 2; i <= n; i++) {
            int spaceNum = (i-1)*2 + 1;
            ans *= spaceNum * (spaceNum + 1) / 2;
            ans %= MODULO;
        }
        return (int) ans;
    }
}