1334. Find the City With the Smallest Number of Neighbors at a Threshold Distance

There are n cities numbered from 0 to n-1. Given the array edges where edges[i] = [fromi, toi, weighti] represents a bidirectional and weighted edge between cities fromi and toi, and given the integer distanceThreshold.

Return the city with the smallest number of cities that are reachable through some path and whose distance is at most distanceThreshold, If there are multiple such cities, return the city with the greatest number.

Notice that the distance of a path connecting cities i and j is equal to the sum of the edges' weights along that path.

Example 1:

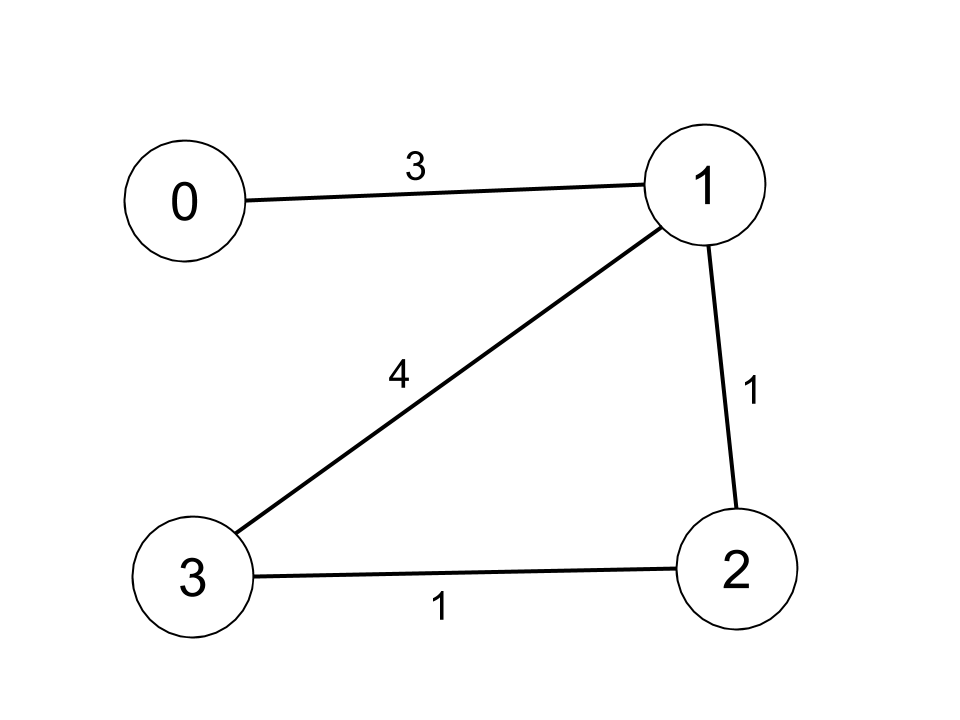
Input: n = 4, edges = [[0,1,3],[1,2,1],[1,3,4],[2,3,1]], distanceThreshold = 4
Output: 3
Explanation: The figure above describes the graph. 
The neighboring cities at a distanceThreshold = 4 for each city are:
City 0 -> [City 1, City 2] 
City 1 -> [City 0, City 2, City 3] 
City 2 -> [City 0, City 1, City 3] 
City 3 -> [City 1, City 2] 
Cities 0 and 3 have 2 neighboring cities at a distanceThreshold = 4, but we have to return city 3 since it has the greatest number.

Example 2:

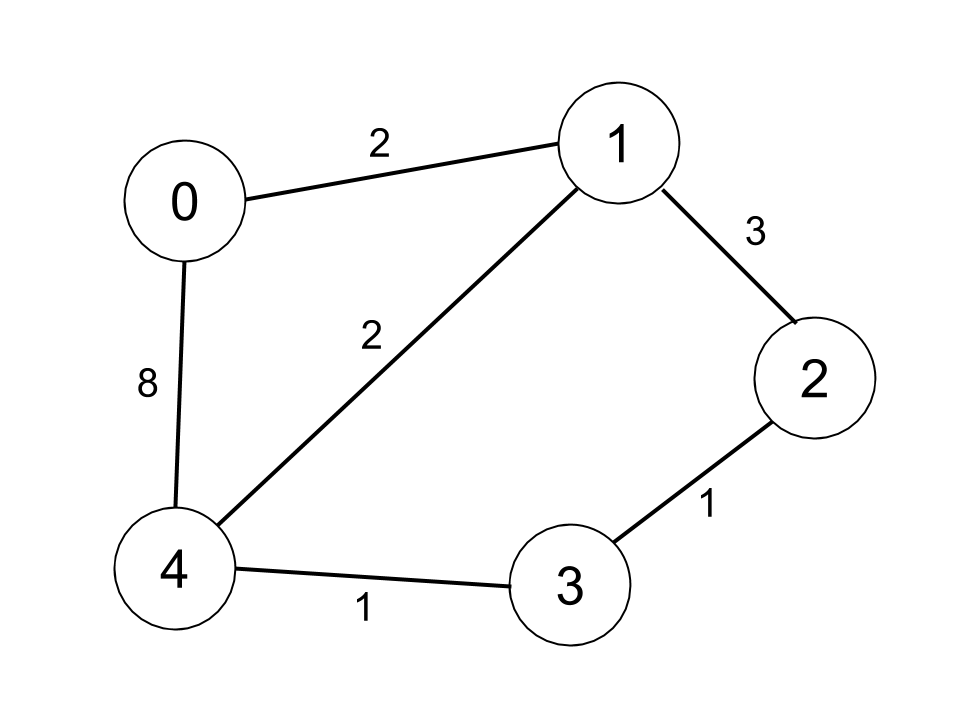
Input: n = 5, edges = [[0,1,2],[0,4,8],[1,2,3],[1,4,2],[2,3,1],[3,4,1]], distanceThreshold = 2
Output: 0
Explanation: The figure above describes the graph. 
The neighboring cities at a distanceThreshold = 2 for each city are:
City 0 -> [City 1] 
City 1 -> [City 0, City 4] 
City 2 -> [City 3, City 4] 
City 3 -> [City 2, City 4]
City 4 -> [City 1, City 2, City 3] 
The city 0 has 1 neighboring city at a distanceThreshold = 2.

Constraints:

• 2 <= n <= 100
• 1 <= edges.length <= n * (n - 1) / 2
• edges[i].length == 3
• 0 <= fromi < toi < n
• 1 <= weighti, distanceThreshold <= 10^4
• All pairs (fromi, toi) are distinct.

public int findTheCity(int n, int[][] edges, int distanceThreshold) {
        int[][] dis = new int[n][n];
        int res = 0, smallest = n;
        for (int[] row : dis)
            Arrays.fill(row, 100000);
        for (int[] e : edges)
            dis[e[0]][e[1]] = dis[e[1]][e[0]] = e[2];
        for (int i = 0; i < n; ++i)
            dis[i][i] = 0;
           
        for(int i = 0; i < n; i++){
                for(int j = 0; j < n; j++){
                    System.out.print(dis[i][j] + " ");
                }
            System.out.println();
        }
        for (int k = 0; k < n; ++k)
            for (int i = 0; i < n; ++i)
                for (int j = 0; j < n; ++j)
                    dis[i][j] = Math.min(dis[i][j], dis[i][k] + dis[k][j]);
           
        for(int i = 0; i < n; i++){
                for(int j = 0; j < n; j++){
                    System.out.print(dis[i][j] + " ");
                }
            System.out.println();
        }
           
        for (int i = 0; i < n; i++) {
            int count = 0;
            for (int j = 0; j < n; ++j)
                if (dis[i][j] <= distanceThreshold)
                    ++count;
            if (count <= smallest) {
                res = i;
                smallest = count;
            }
        }
        return res;
    }

https://leetcode.com/problems/find-the-city-with-the-smallest-number-of-neighbors-at-a-threshold-distance/discuss/490312/JavaC%2B%2BPython-Easy-Floyd-Algorithm

Floyd warshall算法的应用

初始化的顺序应该是：最大值（一般值）-- 0或edges。

初始化的时候要注意是不是无向图，如果是的话要写成dist[i][j]  = dist[j][i] = w