115. Distinct Subsequences

Given a string S and a string T, count the number of distinct subsequences of S which equals T.

A subsequence of a string is a new string which is formed from the original string by deleting some (can be none) of the characters without disturbing the relative positions of the remaining characters. (ie, "ACE" is a subsequence of "ABCDE" while "AEC" is not).

Example 1:

Input: S = "rabbbit", T = "rabbit"
Output: 3
Explanation:

As shown below, there are 3 ways you can generate "rabbit" from S.
(The caret symbol ^ means the chosen letters)

rabbbit
^^^^ ^^
rabbbit
^^ ^^^^
rabbbit
^^^ ^^^

Example 2:

Input: S = "babgbag", T = "bag"
Output: 5
Explanation:

As shown below, there are 5 ways you can generate "bag" from S.
(The caret symbol ^ means the chosen letters)

babgbag
^^ ^
babgbag
^^    ^
babgbag
^    ^^
babgbag
  ^  ^^
babgbag
    ^^^

class Solution {
    public int numDistinct(String s, String t) {
        int m = t.length();
        int n = s.length();
        int[][] dp = new int[m + 1][n + 1];
        
        for(int j = 0; j <= n; j++){
                dp[0][j] = 1;
        }
        for(int i = 1; i <= m; i++){
            for(int j = 1; j <= n; j++){
                dp[i][j] = dp[i][j - 1] + (t.charAt(i-1) == s.charAt(j-1) ? dp[i - 1][j - 1] : 0);
            }
        }
        return dp[m][n];
    }
}

分析如下：

动态规划题目。

以S ="rabbbit",T = "rabbit"为例）：

  

 

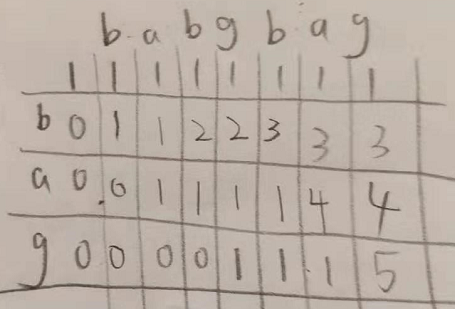
dp[i][j]表示T的从0开始长度为i的子串和S的从0开始长度为j的子串的匹配的个数。

比如, dp[2][3]表示T中的ra和S中的rab的匹配情况。

(1)显然，至少有dp[i][j] = dp[i][j - 1]. 

比如, 因为T 中的"ra" 匹配S中的 "ra"， 所以dp[2][2] = 1 。 显然T 中的"ra" 也匹配S中的 "rab"，所以s[2][3] 至少可以等于dp[2][2]。

(2) 如果T[i-1] == S[j-1]， 那么dp[i][j] = dp[i][j - 1] + (T[i - 1] == S[j - 1] ? dp[i - 1][j - 1] : 0)；

比如, T中的"rab"和S中的"rab"显然匹配，

根据(1)， T中的"rab"显然匹配S中的“rabb”，所以dp[3][4] = dp[3][3] = 1， 

根据(2),   T中的"rab"中的b等于S中的"rab1b2"中的b2, 所以要把T中的"rab"和S中的"rab1"的匹配个数累加到当前的dp[3][4]中。 所以dp[3][4] += dp[2][3] = 2;

(3) 初始情况是
dp[0][0] = 1; // T和S都是空串.
dp[0][1 ... S.length() ] = 1; // T是空串，S只有一种子序列匹配。
dp[1 ... T.length() ][0] = 0; // S是空串，T不是空串，S没有子序列匹配。
————————————————
版权声明：本文为CSDN博主「feliciafay」的原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/feliciafay/article/details/42959119