吉普赛人的祖传小把戏读心术

被震住了

今天下午回来后玩了一个小游戏，吉普赛人祖传的神奇读心术，相信园子里很多同学都玩过了，刚开始玩真被震住了，想什么来什么，太牛了。甚至心里有点害怕了，不过仔细想了一下，原来如此。呵呵。

地址：http://www.soche8.com/info/yule/dxs.html，游戏截图如下：

当你心中想着从10-99这样的两位数时，如果想到了比如23，那么就要用23减去个位和十位相加的和，即23-（2+3）=18，然后看一下18这个数字在右边的表格中对应的图标是什么样子的，再点击一下圆球会发现，呀，居然显示了我心中想象的那个图。太神奇了，给朋友看时他们也觉得太可怕了，居然知道我们心中想的是什么。

怀疑&求解

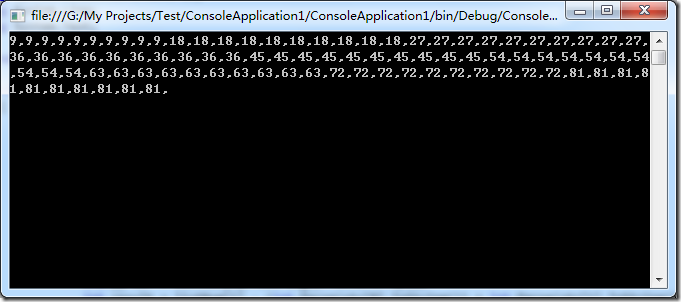
咱毕竟是做计算机科学的，这玩意就是个数字游戏，咋回事呢，分析了一下，首先要从这个公式入手，先啥也不想，将这个公式挑选出来的数字选出来看看啥规律吧，于是从10-99这90个数字，我们做循环，输出得到的结果：

 1 using System; 
 2 using System.Collections.Generic; 
 3 using System.Linq; 
 4 using System.Text; 
 5 
 6 namespace ConsoleApplication1 
 7 { 
 8     class Program 
 9     { 
10         static void Main(string[] args) 
11         { 
12             List<int> listNum = new List<int>(); 
13             for (int i = 10; i < 100;i++ ) 
14             { 
15                 listNum.Add(i); 
16             } 
17 
18             for (int i = 0; i < listNum.Count;i++ ) 
19             { 
20                 char[] str = listNum[i].ToString().ToCharArray(); 
21                 int result = listNum[i] - (int.Parse(str[0].ToString()) + int.Parse(str[1].ToString())); 
22                 Console.Write(result+","); 
23             } 
24             Console.ReadLine(); 
25         } 
26     } 
27 }
28 

经过这个输出，我们不难发现，从10-99这90个数经过这个：23-（2+3）=18公式计算后，得到的结果都是9的倍数，也就是说，只要在10-99中间你任意想一个数，都是9的倍数，那么我只需要将9的倍数的数字对应的图标调整成一样的图片即可，再观察一下这个游戏的右边给出的表中，呵呵，果然如此。

那么，这个算法是怎么来的呢，我们来看看，因为是10-99之间的数，我们可以表示为(10*a+b)-(a+b)=9a,呵呵，看到了吧，10*a+b这个公式便能表示为10-99之间的任意一个数，运算后都是9的倍数。