1438：灯泡

 1438：灯泡（一本通网站原题链接)

【分析】

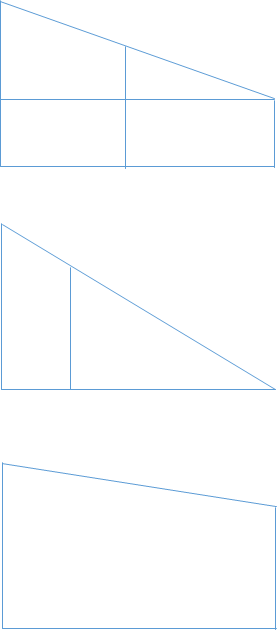
　　这个题其实我想说就是一个数学题，借助电脑比用笔算更简单的数学题。如右图，我画了三个图，倒着看吧，最后一个图最简单，人就靠墙站了，这时人的影子长等于人的高度h，这意味着影子的长最少是人的高度。其次是第二个图影子的末尾刚好是墙根，根据我这个图的数据应该比人的高度要大，当然数据给得不同结果他不同。这个图也是任何数据下可以实现的，那么影子的长度至少可以取这两种情况的最大值。还有一种情况就是第一图。那就是在第二图的基础上，人继续靠墙走，这时人的影子分为两部分，一部分在地上一部分在墙上，如图，做一条平行于地面的辅助线，上面两个三角形是相似，可以设人与灯的水平距离为x，墙上影子长度为y，那么(D-x):D=(h-y):(H-y)并由此算出y=H-(H-h)D/x，影子总长为D-x+y=D+H-[x+(H-h)D/x]<=D+H-2sqrt[(H-h)D]，当x=sqrt[(H-h)D]时取到等号。也就是说这个最大值需要在条件满足时还会有，不满足就不会有。x本身的范围首先是[0,D]，其实要出现第一图，人站的位置应该比第二图更靠近墙，那x>=D-Dh/H。如果这两个条件(D-Dh/H<=sqrt[(H-h)D]<=D)都满足就有第三个最大值。当然，最后这些最大值取最大值就OK了。余下的就是变成代码了。

//1438：灯泡
#include<iostream>
#include<cmath>
#include<iomanip>
using namespace std;
int n;
double H,h,D;
double calc()
{
    double ans=0;
    if(H-h<=D&&(H-h)*D<=H*H)
        ans=D+H-2*sqrt((H-h)*D);//这个最大值是有条件的
    if(ans<h)ans=h;//这是靠墙站时的最大值，无条件
    if(ans<D*h/H)ans=D*h/H;//这是影子全在地面的最大值，总可以满足
    return ans;
}
int main(){
    cin>>n;
    while(n--)
    {
        cin>>H>>h>>D;
        cout<<fixed<<setprecision(3)<<calc()<<endl;
    }
    return 0;
}