线性最小二乘法的矩阵解法

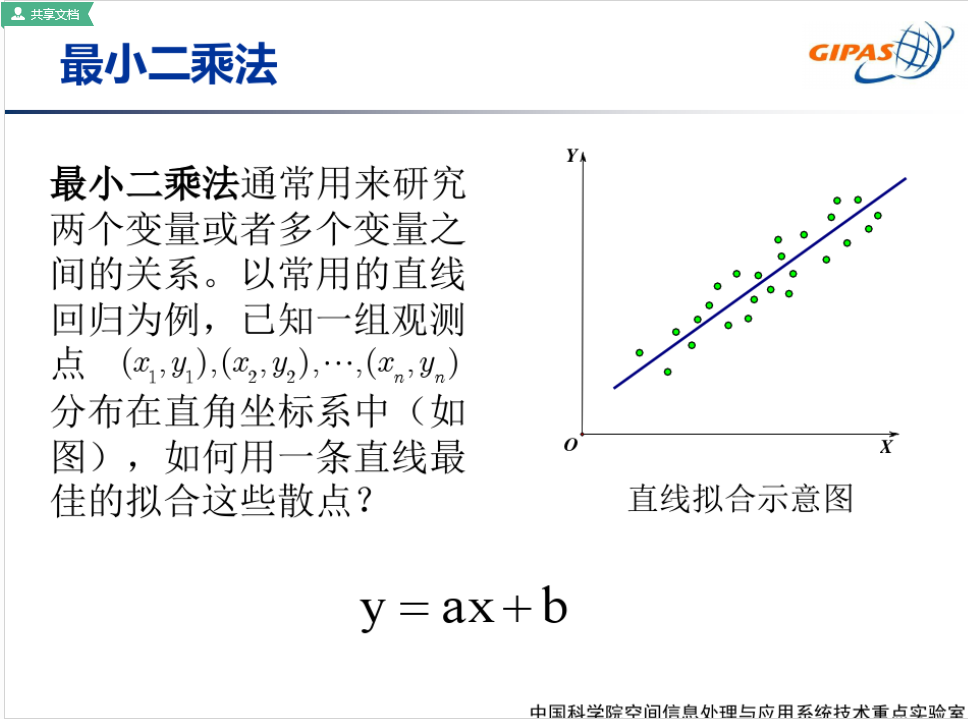
1.公式推导

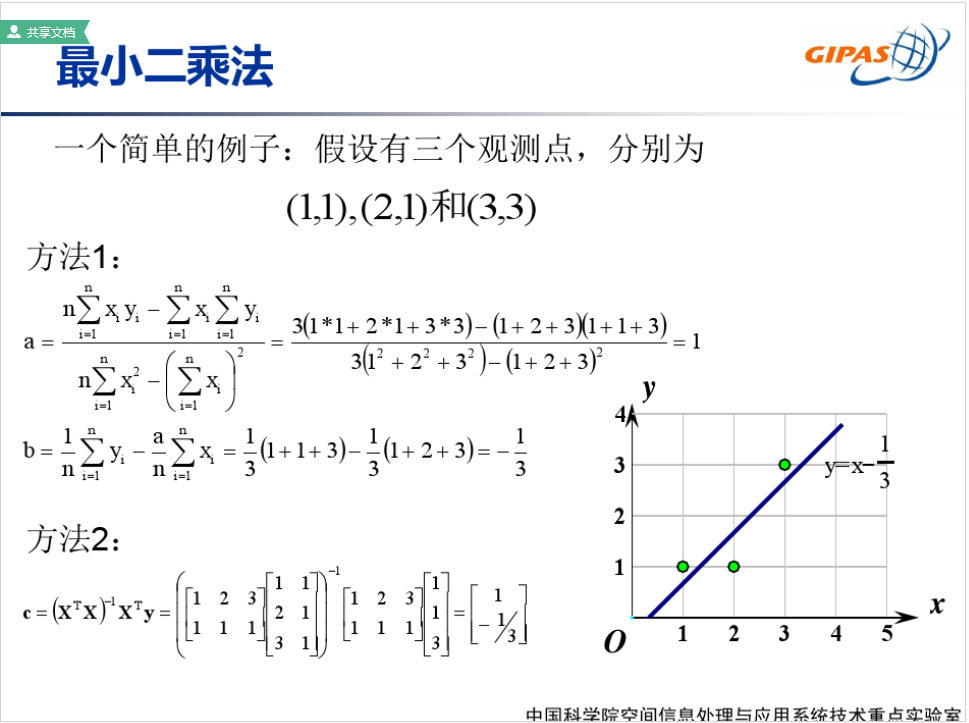
PPT参考自：中国科学院的PPT ，矩阵解的具体推导过程见博客。

其中残差函数矩阵 f(c) 求导的过程推导如下，需要用到矩阵求导的2条结论

 

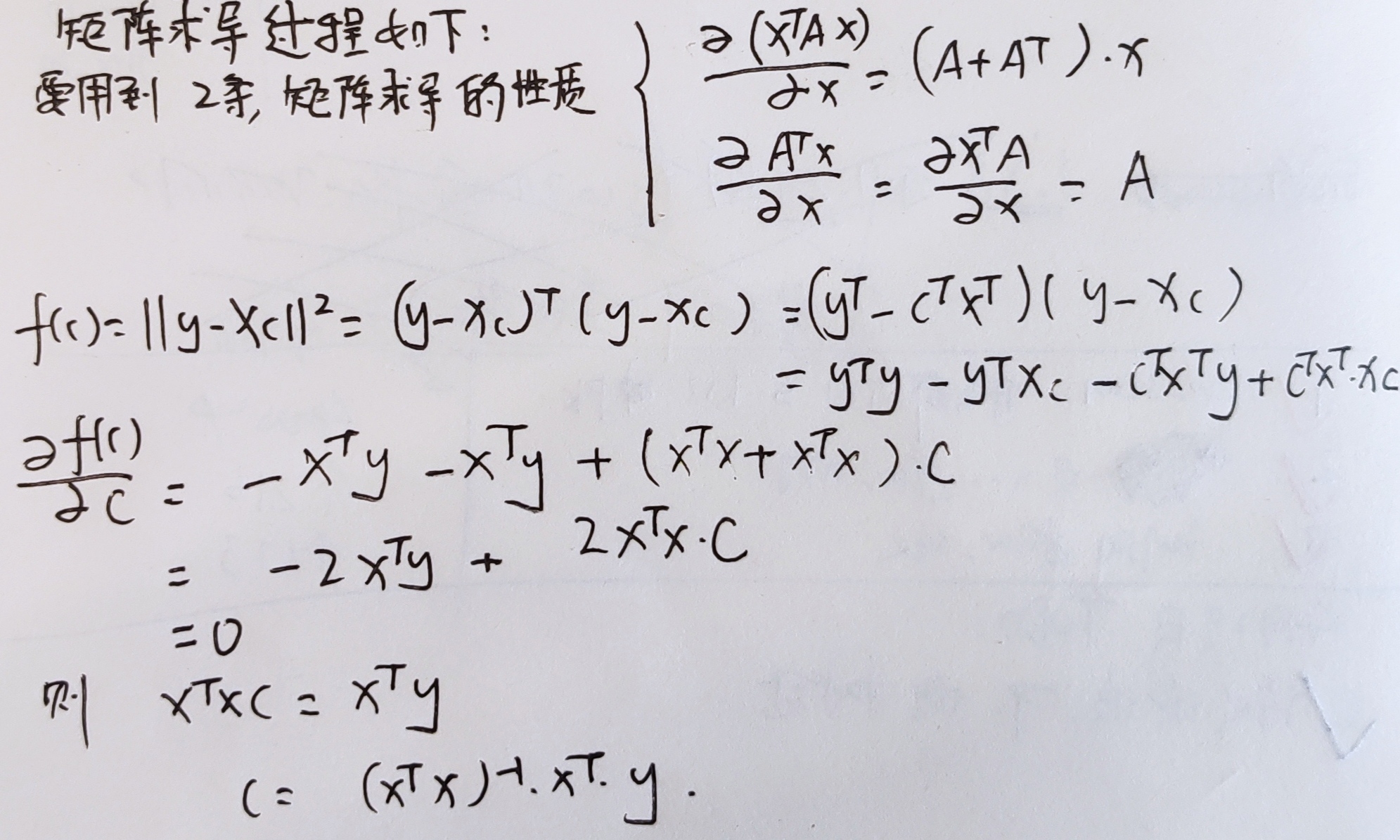
2.两种最小二乘法的平面拟合MATLAB代码对比

1）用传统的∑方式求平面方程z=ax + by + c的参数

function [ a,b,c ]=FitPlane( input_X , input_Y , input_Z)

% FileName   : FitPlane
% CreatDate  : 2018/7/10
% Describe    : Least square fitting plane equation
% OutputPara : a,b,c
% Note         : Plane equation: z=a*x+b*y+c
% Author       : wellp

X1=0;Y1=0;Z1=0;X2=0;Y2=0;X1Y1=0;X1Z1=0;Y1Z1=0;
num=length(input_X);
if num<3 % less than 3 points can't fit the plane
    a=-8888;
    b=-8888;
    c=-8888;
else
for i=1 : num
    X1=X1+input_X(i);
    Y1=Y1+input_Y(i);
    Z1=Z1+input_Z(i);
    X2=X2+input_X(i)^2;
    Y2=Y2+input_Y(i)^2;
    X1Y1=X1Y1+input_X(i)*input_Y(i);
    X1Z1=X1Z1+input_X(i)*input_Z(i);
    Y1Z1=Y1Z1+input_Y(i)*input_Z(i);
end

N=num;
C=N*X2-X1*X1;% X2!=X1*X1 !!!!!!!
D=N*X1Y1-X1*Y1;
E=-(N*X1Z1-X1*Z1);
G=N*Y2-Y1*Y1;
H=-(N*Y1Z1-Y1*Z1);

a=(H*D-E*G)/(C*G-D*D);
b=(H*C-E*D)/(D*D-G*C);
c=(Z1-a*X1-b*Y1)/N;

end
end

2）用矩阵的形式求解同样的问题。用多组示例测试，2）求出的Xpara确实等于1）求出的 [a, b, c]。

function [ Xpara ]=FitPlane( input_X , input_Y , input_Z)
% FileName   : FitPlane
% CreatDate  : 2018/7/10
% Describe    : Least square fitting plane equation
% OutputPara : Xpara
% Note         : Plane equation: z=a*x+b*y+c
% Author       : wellp

X = input_X';
Y = input_Y';
I = ones(size(input_X'));
A = [X, Y, I];
b = input_Z';
Xpara = (A' * A) ^ -1 * A' * b; 

end

苍了天了，矩阵也太TM的简洁了吧，上述问题的矩阵的推导如下：

 

3.线性最小二乘和非线性最小二乘的讨论

1）概念区别

线性最小二乘问题：问题可以抽象成线性数学模型，例如直线拟合 y = ax + b、平面拟合 z = ax + by + c，这类线性问题也就可以写成前述的矩阵形式

非线性最小二乘问题：问题为非线性数学模型，无法写成前述的矩阵形式

2）正规方程

对于线性最小二乘问题：为了获得更可靠的结果，测量次数 总要多于未知参数的数目 ，即所得误差方程式的数目总是要多于未知数的数目。因而直接用一般解代数方程的方法是无法求解这些未知参数的。最小二乘法则可以将误差方程转化为有确定解的代数方程组（其方程式数目正好等于未知数的个数），从而可求解出这些未知参数。这个有确定解的代数方程组称为最小二乘法估计的正规方程（或称为法方程）。

3）解法区别

线性最小二乘问题：

a.可以直接通过对残差函数求导数（偏导），令导数（偏导）等于0获得残差函数的极小值，进而解得待求参数

b.如果问题写成了前述的矩阵形式，则求解矩阵即可。当参数矩阵较小时，可以直接解前述的正规方程A^TAx=A^Tb，x = (A^TA)^-1A^Tb进行求解；当参数矩阵较大时，求逆矩阵的耗时较大，一般通过QR分解，Cholesky分解，SVD分解进行求解。

非线性最小二乘问题：

无法直接写出导数或者导数过于复杂；因为无法写成矩阵的形式，也无法通过上述矩阵分解的方法求解。一般通过一阶梯度法（最速下降法）、二阶梯度法（牛顿法）、高斯牛顿法、LM（Levenberg-Marquardt Method）法进行迭代求解。