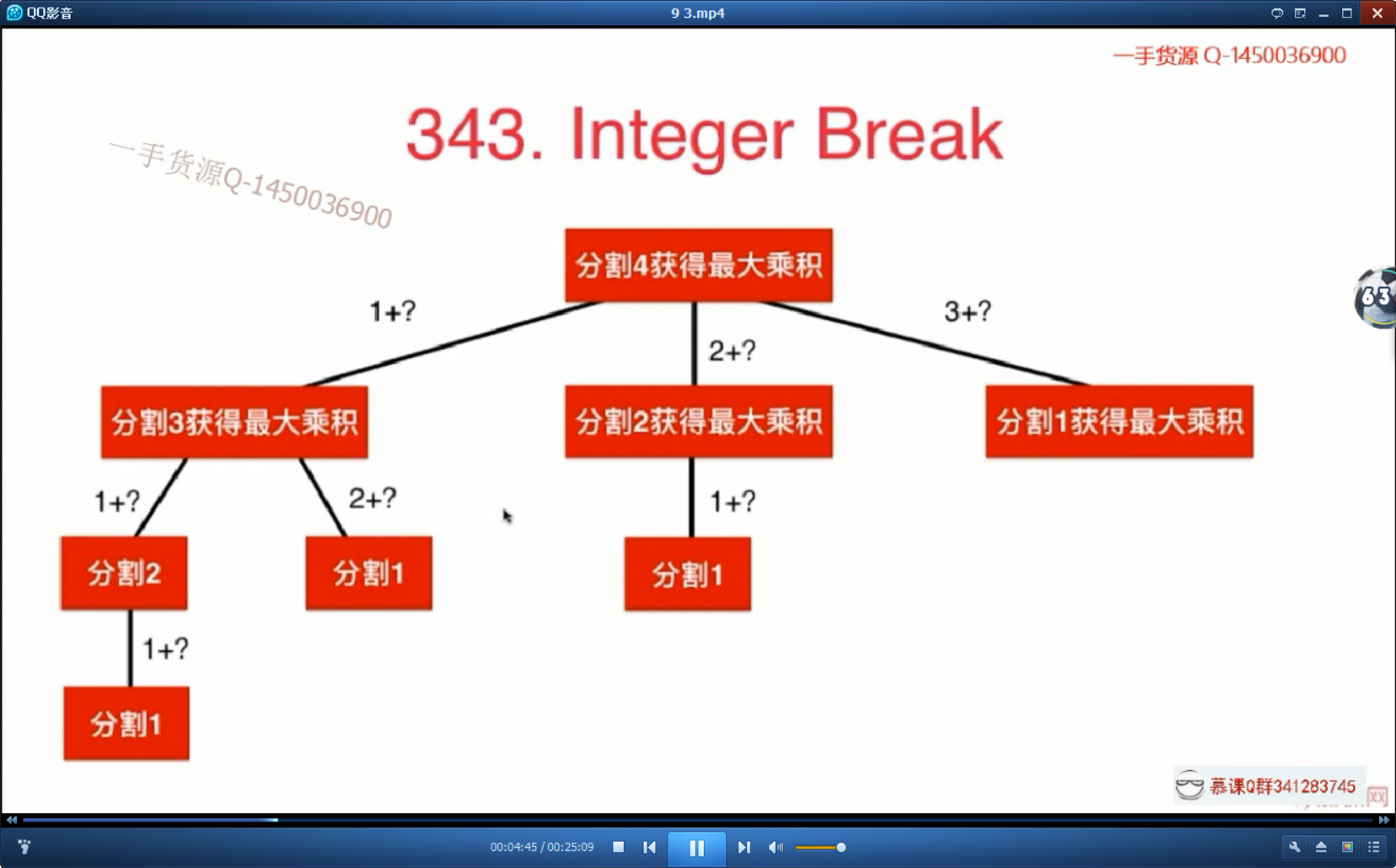

大量的重复子问题
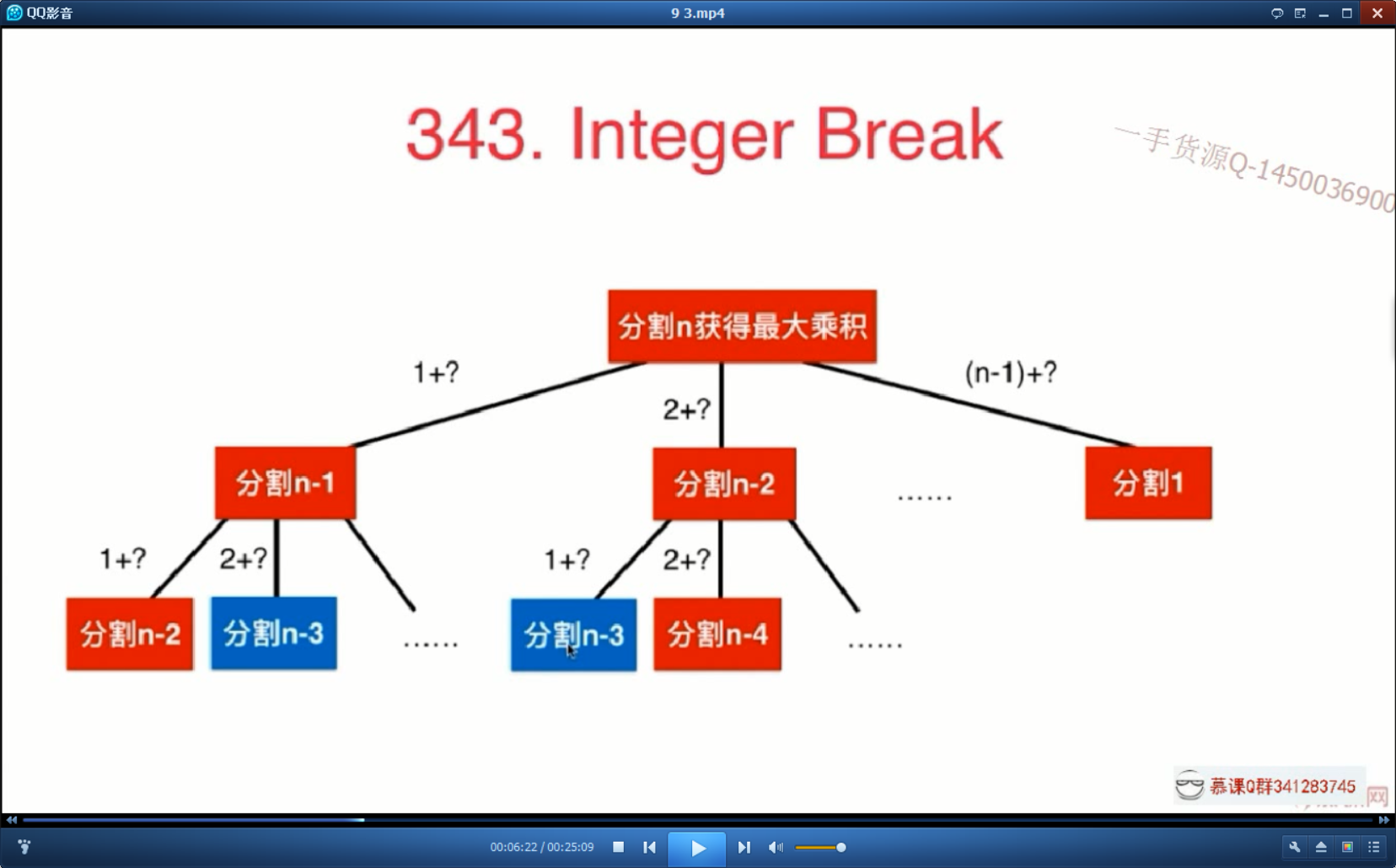
通过解决n-1,n-2,n-3 ······· 1等子问题就能解决原问题。
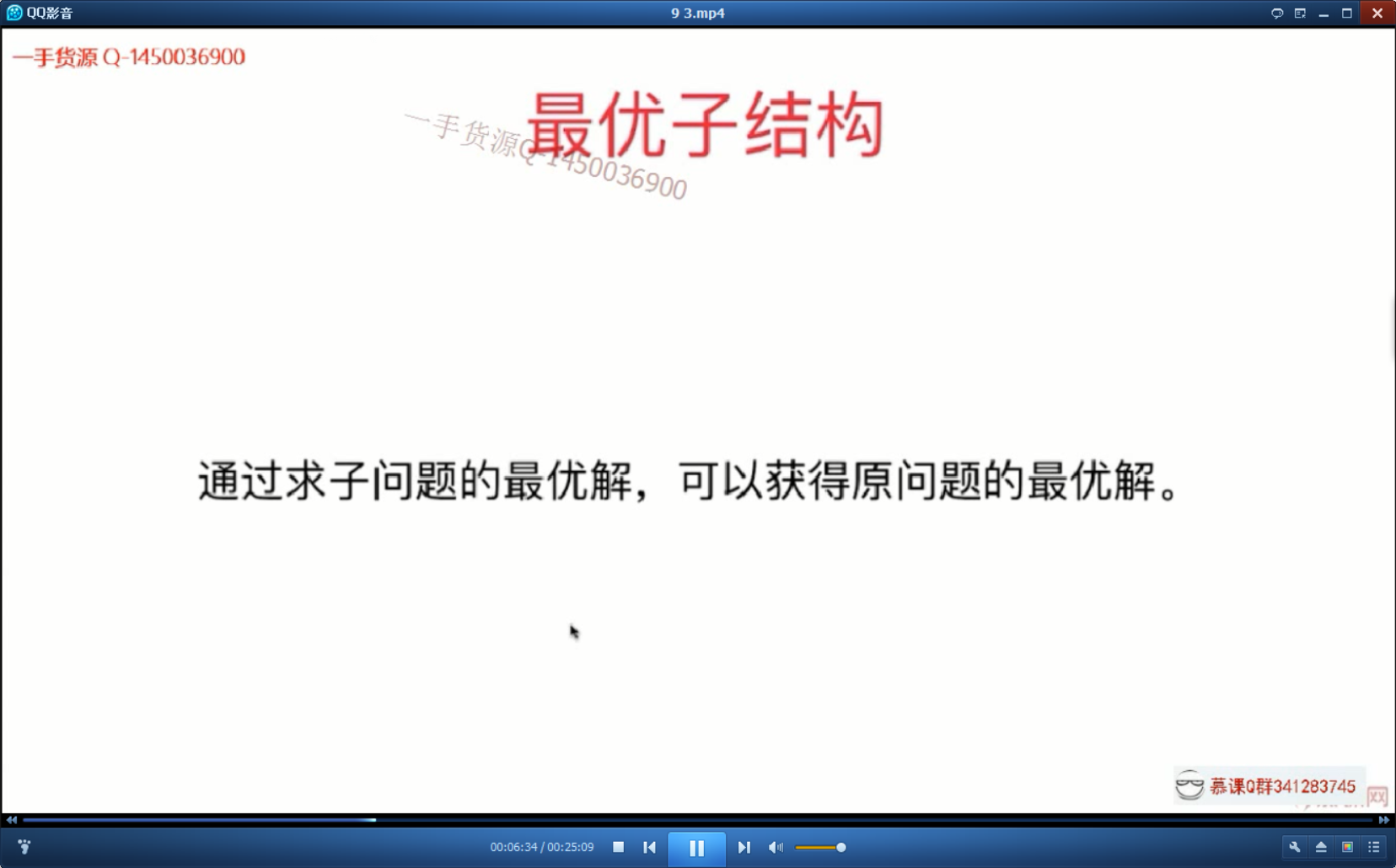
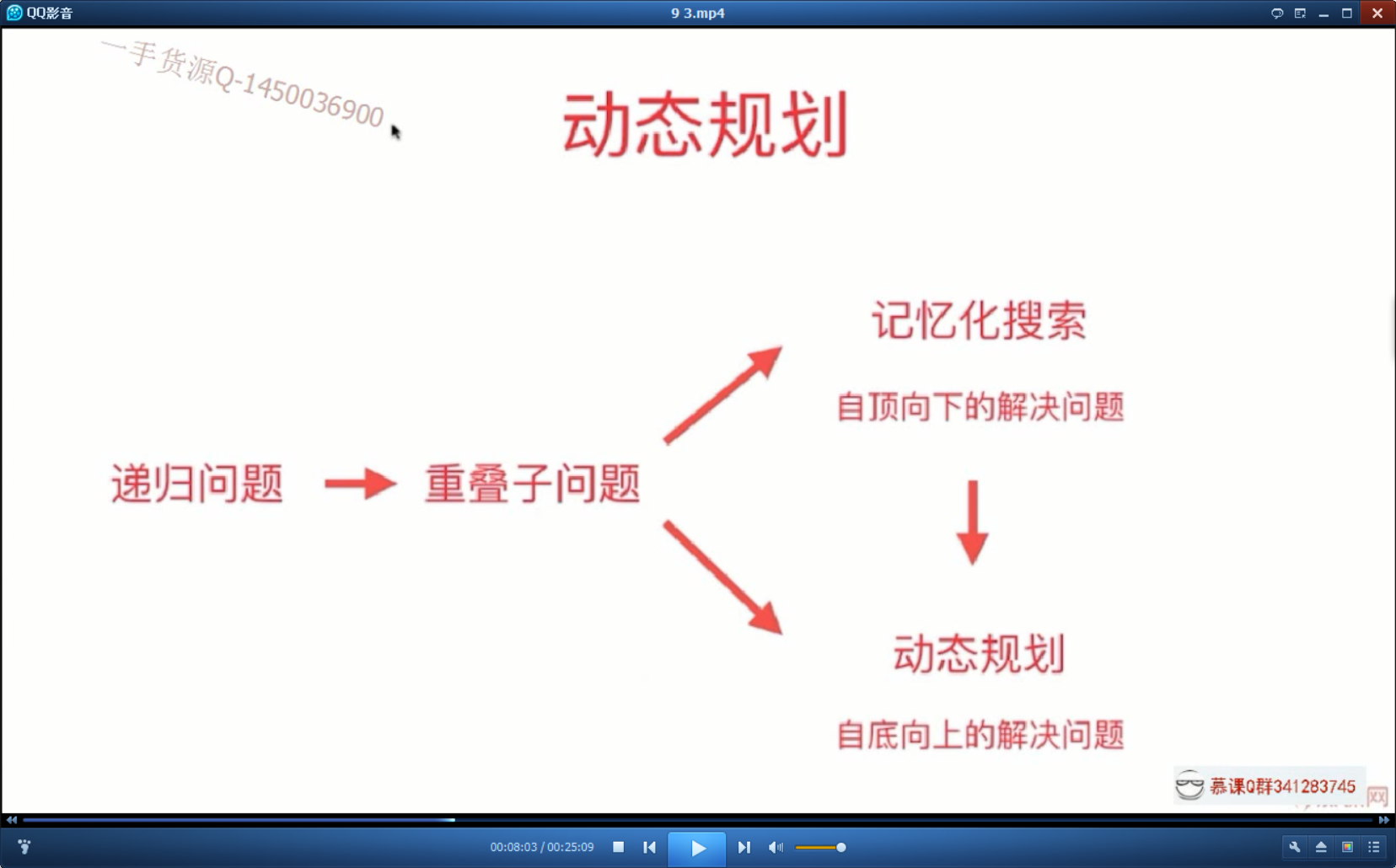
如果一个题目,能够通过解决自问题就能找到答案,那么就能动态规划!
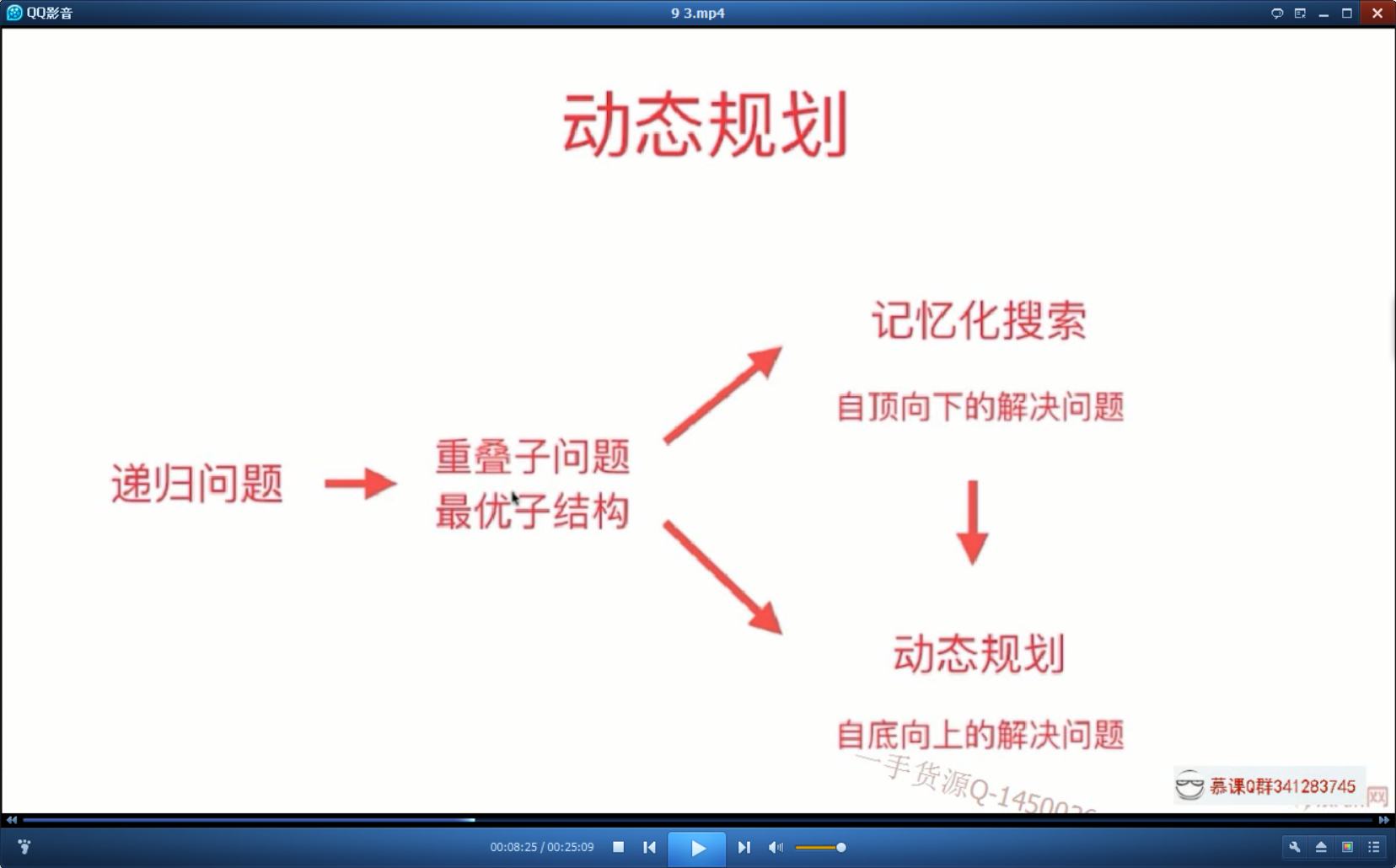
递归写法

记忆化搜索

动态规划写法

但是还是平方级别的
我的代码
其实就是比较j*(i-j)和j*memo【i-j】
因为分解出来是对称的,前面已经计算过1*xxx了后面就不用计算xxx*1了,刚好1不需要遍历
private int memo[]; public int integerBreak(int n) { memo = new int[n+1]; //基础问题 1 的值对应什么? 1 还是不要遍历了,memo【1】没法填。。。 memo[2]=1; //对于3-n的每个值,填memo数组,对应的是该值的解 for(int i=3;i<=n;i++){ int max = 0; //因为不遍历1,所以j要到i-1之前就停止 for(int j=1;j<i-1;j++){ //计算j*(i-j) int temp1 = j*(i-j); int temp2 = j*memo[i-j]; //因为memo【n】不一定比n大,比如2和3 //memo【n】是n分割乘积的最大值,也就是别的组合里面最大值 int tempMax = temp1; if(temp2>tempMax) tempMax=temp2; if(tempMax>max) max=tempMax; } memo[i]=max; } return memo[n];
舒服

一次通过美滋滋

279
91
62
和64号问题很像,也是一个数组从【m】【n】回填到【0】【0】即可
基本是简化版的64,因为最后和最右都是1.
public int uniquePaths(int m, int n) { int [][] matrix = new int[m][n]; //从最后一个开始,最后一行,最后一烈,这样逆序,一直到【0】【0】 for(int i=m-1;i>=0;i--){ for(int j=n-1;j>=0;j--){ if(i==m-1&&j==n-1){ matrix[i][j]=1; }else if(i==m-1){ //最后一行,无论如何都是只有一种走法,就是往右走 matrix[i][j]=1; }else if(j==n-1){ //最右列也只有一直往下走 matrix[i][j]=1; }else{ //其他就是右边的方法数加上右边的方法数 int right = matrix[i][j+1]; int next = matrix[i+1][j]; matrix[i][j]=right+next; } } } return matrix[0][0]; }

一次嘻嘻
63
这个其实也不是难了很多
先遍历,将1变成-1,障碍都用-1表示。
依旧是以前那样,从后面填。
如果右边或下边是-1的,就将这边的路径当作0就好了。
这个题目我没有一次过,主要是漏了几个情况。
1、开始或终点就是障碍物,这种直接返回0,就是无法到达。
2、如果最后一行的右边不是-1,那么就设为1。错了啊,右边还可能是0呢。
3、忘了判断这个数本身是不是-1.
最后修改的代码,不是很优雅,但是思路能看清。
//如果开始就是1,直接就不可能了 if(obstacleGrid[0][0]==1) return 0; //行 int row = obstacleGrid.length; //列 int col = obstacleGrid[0].length; //如果终点是1,也是不可能的 if(obstacleGrid[row-1][col-1]==1) return 0; for(int i=0;i<row;i++){ for(int j=0;j<col;j++){ if(obstacleGrid[i][j]==1) obstacleGrid[i][j]=-1; } } //从后面设置起 for(int i=row-1;i>=0;i--){ for (int j=col-1;j>=0;j--){ if(i==row-1&&j==col-1){ obstacleGrid[i][j]=1; }else if(i==row-1){ //看自己是不是-1 if(obstacleGrid[i][j]==-1) continue; //最后一行,要看右边是不是-1 if(obstacleGrid[i][j+1]==-1) obstacleGrid[i][j]=0; else //右边有可能是0 obstacleGrid[i][j]=obstacleGrid[i][j+1]; }else if(j==col-1){ //看自己是不是-1 if(obstacleGrid[i][j]==-1) continue; //最右一列,看看下边是不是-1 if(obstacleGrid[i+1][j]==-1) obstacleGrid[i][j]=0; else //下边有可能是0 obstacleGrid[i][j]=obstacleGrid[i+1][j]; }else{ if(obstacleGrid[i][j]==-1) continue; else{ int right = obstacleGrid[i][j+1]; int next = obstacleGrid[i+1][j]; if(right!=-1) obstacleGrid[i][j]+=right; if(next!=-1) obstacleGrid[i][j]+=next; } } } } return obstacleGrid[0][0];