最近由于.......你懂得,需要一些搜索方面的知识,于是乎我重新复习了一下上半年读的那本书《数学之美》Dr吴军老师写的。
感觉读完这种书还是写一下比较好,因为将来说不定就会忘记了。
接下来几篇就像写一下搜索算法的各种原理了。
虽然在公司我们使用过solr,虽然使用solr之前也知道Solr使用的是tf-idf值来建立的索引。但这只是庞大搜索体系中的一个小部分,
里面的内容还是很多的。
下面废话就不多说了,咱们开始讲PageRank算法的计算方法啦。
PageRank算法的核心思想是:
在互联网上,如果一个网页被很多其他网页所链接,说明它收到普遍的承认和信赖,那么它的排名就高。这就是PageRank的核心思想
是由谷歌的创始人 拉里佩奇 和 谢尔盖布林 一起发明的。个人觉得就是天才啊
PageRank的计算方法:
假定向量B=(b1,b2,......,bN)T为第一,第二,第N个网页的网页排名。矩阵
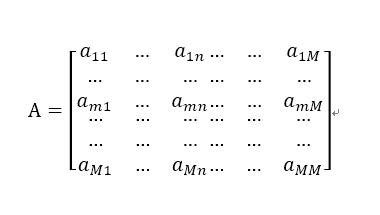
为网页之间连接的数目,其中amn代表第m个网页指向第n个网页的链接数。
A是已知的,B是未知的,是我们所要计算的。
假定Bi是第i次迭代的结果,那么
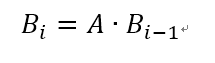 (10-3)
(10-3)
初始假设:所有网页的排名都是1/N,即
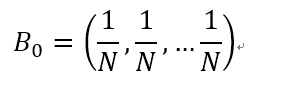
显然通过(10-3)简单(但是计算量非常大)的矩阵运算,可以得到B1,B2.... 可以证明最终Bi会收敛,即Bi无限趋近于B,
此时:B=B*A
因此当两次迭代的结果Bi和Bi-1之间的差异非常小,接近于0时,停止迭代运算,算法结束。
一般来讲,只要10次左右的迭代基本上就收敛了
由于网页之间连接的数量相比互联网的规模非常稀疏,因此计算网页的排名也需要对0概率或者小概率事件进行平滑处理。
网页的排名是一个一维向量,对它的平滑处理只能利用一个小的常熟α 这时公式变成如下:
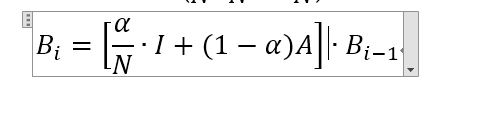
其中N是互联网网页的数量
α 是一个较小的常数。I是单位矩阵。
网页排名的计算主要是矩阵相乘,这种计算很容易分解成许多小任务,在多台计算机上进行并行处理。就是MapReduce