递归算法应用

一、递归的定义

1. 递归就是程序在运行的过程中调用自己（用自己定义自己）
递归的三要素：
1. 边界条件
2. 递归前进段
3. 递归返回段
2. 递归和栈

　　　　递归和栈有这紧密的联系，大多数编译器都是使用栈来实现递归的，当调用方法时，编译器会把这个方法的所有参数和返回地址都压入栈中，然后把控制转移给这个方法。当方法返回时，这些值退栈。参数消失了，并且控制权重新回到返回地址处。

　　　　调用一个方法时，所进行的步骤：

　　　　1）当一个方法被调用时，它的参数和返回地址压入栈中

　　　　2）这个方法可以通过获取栈顶元素访问参数

　　　　3）当这个方法返回时，它查看栈已获取返回地址，然后这个地址和所有参数退栈，并且销毁

　　下图是求阶乘的图示，帮助理解：

　　

二、求整数n的阶乘　

/**
     * 求整数n的阶乘
     *
     * @param n 整数n
     * @return
     */
    public static int factorial(int n) {
        if (n < 0) {
            return -1;//返回-1证明参数有问题
        }
        if (n == 1 || n == 0) {
            return 1;
        } else {
            return n * factorial(n - 1);
        }
    }

三、在有序数组中查找目标值（二分法）

 /**
     * 二分法递归,找目标值位置
     * 查找的数组一定是有序的
     * @param array  有序数组
     * @param start  起始位置
     * @param end    结束位置
     * @param target 目标值
     * @return 返回-1代表没找到目标值
     */

    public static int dichotomy(int[] array, int start, int end, int target) {
        int mid = start + (end - start) / 2;
        if (array[mid] == target) {
            return mid;
        } else if (start >= end) {
            return -1;
        } else if (array[mid] > target) {
            dichotomy(array, start, mid - 1, target);
        } else if (array[mid] < target) {
            dichotomy(array, mid + 1, end, target);
        }
        return -1;
    }

四、汉诺塔问题

　　汉诺塔问题是一个经典的问题。汉诺塔（Hanoi Tower），又称河内塔，源于印度一个古老传说。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，任何时候，在小圆盘上都不能放大圆盘，且在三根柱子之间一次只能移动一个圆盘。问应该如何操作？

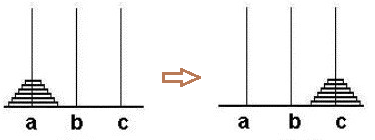
 问题分析：

　　假设a最下边的盘子为n，如果想把n移动到目标c上，需要先把n-1到n的盘子整体挪到b上，再把n移到c上。此时将b和a交位置，忽略c上的盘子，则移动n个盘子的问题转变为移动n-1个盘子的问题。依次类推，最终简化为移动两个盘子的问题。

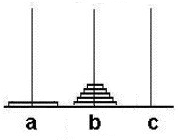
 总结规律：

　　移动n个盘子所需的总步骤为：2ⁿ-1步

代码实现：

   /**
     * 汉诺塔问题
     * @param n    盘子个数(也表示名称)  盘子从大->小编号依次为 1->n
     * @param from 初始塔座
     * @param temp 中介塔座
     * @param to   目标塔座
     */
    public static void hanoi(int n, String from, String temp, String to) {
        if (n == 1) {
            move(from, to);
        } else {
            hanoi(n - 1, from, to, temp);
            move(from, to);
            hanoi(n - 1, temp, from, to);
        }
    }

    public static void move(String from, String to) {
        log.info("从 {} 移动到 {}", from, to);
    }

五、求乘方

　　计算x^y相当于y个x相乘，用二分法的思想，每次都将y分成两半，此时就有奇偶的问题需要注意。

　　代码实现如下：

　　

   /**
     *  求 num 的 pow次方
     */
    public static int mypow(int num, int pow) {
        if (num == 0 || num == 1 || pow == 0) {
            return 1;
        }
        if (pow % 2 == 1) {
            return num * mypow(num, pow / 2) * mypow(num, pow / 2);
        } else {
            return mypow(num, pow / 2) * mypow(num, pow / 2);
        }
    }

六、背包问题

　　问题：有多种不同重量的背包，假如你想要一个20kg背包，你可以有多种选择方式。

　　解析：其实这是一个排列组合问题，将背包按任意顺序排列A、B、C、D、E，从第一个背包开始，此时你有两个选择，要么选择A要不不选择A，选择A的话你需要从剩下的背包里选20-A的重量，不选择A的话你需要从剩下的背包里选择20的重量。不论你是否选择A背包，你面对背包B的时候同样面临两个选择，以此类推，当你遍历到最后一个背包时已经遍历的所有的场景。当你需要从剩下的背包中选择0的重量时，说明你现在选择的背包满足要求，不能再选。当你需要从剩下的背包中选择负数的重量时，说明你如果选择现有的背包，那么你不可能选到符合要求的背包，需要跳过。

　　代码实现：　

public class Knapsack {

    private int[] weights;//可供选择的重量

    private Boolean[] selects;//标记是否选择该重量

    private Knapsack(int[] weights) {
        this.weights = weights;
        this.selects = new Boolean[weights.length];
    }

    /**
     * 选择组合方式
     * @param weight 目标重量
     * @param index  开始索引（从第几个开始选，前边的不选）
     */
    private void select(int weight, int index) {
        if (weight == 0) {
            for (int i = 0; i <= index; i++) {
                if (selects[i]) {
                    System.out.print(weights[i] + " ");
                }
            }
            System.out.println();
            return;
        }

        if (weight < 0 || index >= weights.length) {
            return;
        }
        //选择该重量
        selects[index] = true;
        select(weight - weights[index], index + 1);
        //不选择该重量
        selects[index] = false;
        select(weight, index + 1);
    }

    public static void main(String[] args) {
        int[] a = {11, 6, 5, 9, 7};
        Knapsack k = new Knapsack(a);
        k.select(20, 0);
    }

}

　　输出结果:

　　

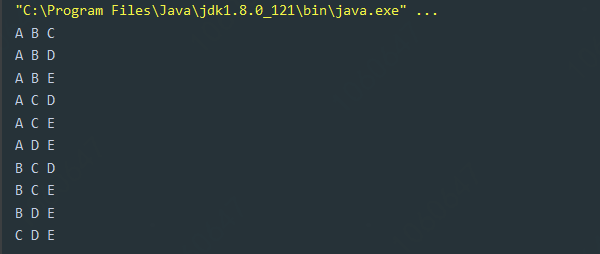
七、选择队友问题

　　从n个人中选择m个人最为你的队友，此问题与背包问题相同，解析方法类似。

　　代码实现：

/**
 * 选择队员
 * 1、从n个人中选择m个队员，例如从5个人中选择3个记录为（5,3）
 * 2、假设从第一个人开始选择，那么分为选择和不选择两种情况，即为（5,3）=（4,2）+（4,3）依次类推
 */


public class SelectTeam {
    private char[] persons; //所有可以选择的人
    private Boolean[] selects; //长度与人数相同，记录每个人是否被选择

    private SelectTeam(char[] persons) {
        this.persons = persons;
        this.selects=new Boolean[persons.length];
    }

    /**
     * 选择队员
     * @param num 要选择的队员数
     * @param index 从第几个开始选
     */
    public void select(int num,int index){

        if (num==0){
            for (int i=0;i<index;i++){
                if (selects[i]){
                    System.out.print(persons[i]+" ");
                }
            }
            System.out.println();
            return;
        }

        if (num < 0 || index > persons.length-1) {
            return;
        }

        //选择第一个人
        selects[index]=true;
        select(num-1,index+1);
        //不选择第一个人
        selects[index]=false;
        select(num,index+1);
    }

    public static void main(String[] args) {
        char[] person=new char[]{'A','B','C','D','E'};
        SelectTeam selectTeam=new SelectTeam(person);
        selectTeam.select(3,0);
    }
}

输出结果：