1.核心思想
如果一个样本在特征空间中的k个最相邻的样本中的大多数属于某一个类别,则该样本也属于这个类别,并具有这个类别上样本的特性。也就是说找出一个样本的k个最近邻居,将这些邻居的属性的平均值赋给该样本,就可以得到该样本的属性。
下面看一个例子,
一个程序员面试结束后,想想知道是否拿到offer,他在网上找到几个人的工作经历和大概薪资,如下,X为年龄,Y为工资;
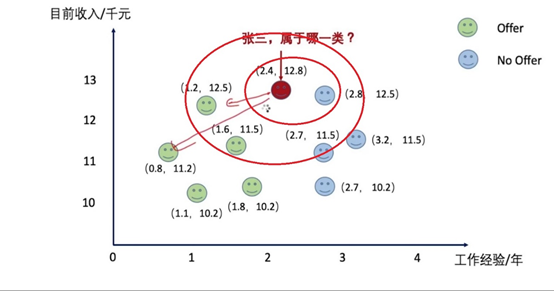
当k取1的时候,我们可以看出距离最近的no offer,因此得到目标点为不被录用。
当k取3的时候,我们可以看出距离最近的三个,分别是有offer 和no offer,根据投票决定 offer的票数较高为2 ,所以被录用。
算法流程
1. 准备数据,对数据进行预处理,常用方法,特征归一化、类别型特征的处理、高维组合特征的处理、组合特征的处理、文本表示模型的模型处理、Word2Vec、图像数据不足时的处理方法
2. 选用合适的数据结构存储训练数据和测试元组,根据模型验证方法,把样本划分不同的训练集和测试集,比如holdout只需要划分为两个部分,交叉验证划分为k个子集,自助法跟着模型来
3. 设定参数,如k的取值,这个涉及到超参数调优的问题,网络搜索、随机搜索、贝叶斯算法等
4.维护一个大小为k的的按距离由大到小的优先级队列,用于存储最近邻训练元组。随机从训练元组中选取k个元组作为初始的最近邻元组,分别计算测试元组到这k个元组的距离,将训练元组标号和距离存入优先级队列
5. 遍历训练元组集,计算当前训练元组与测试元组的距离,将所得距离L 与优先级队列中的最大距离Lmax
6. 进行比较。若L>=Lmax,则舍弃该元组,遍历下一个元组。若L < Lmax,删除优先级队列中最大距离的元组,将当前训练元组存入优先级队列。
7. 遍历完毕,计算优先级队列中k 个元组的多数类,并将其作为测试元组的类别。
8. 测试元组集测试完毕后计算误差率,继续设定不同的k值重新进行训练,最后取误差率最小的k 值。
简单来说,knn算法最重要的是三个要素:K值选择,距离度量,分类决策规则,
K的选择
如k的取值,这个涉及到超参数调优的问题,k的取值对结果会有很大的影响。K值设置过小会降低分类精度,增加模型复杂度;若设置过大,且测试样本属于训练集中包含数据较少的类,则会增加噪声,降低分类效果。通常,K值的设定采用交叉检验的方式(以K=1,K=2,K=3依次进行),K折交叉验证如下:
1) 将全部训练集S分成K个不相交的子集,假设S中的训练样例个数为m,那么每一个子集有m/k个训练样例。
(2) 每次从分好的子集中,选出一个作为测试集,另外k-1个作为训练集。
(3) 根据训练集得到模型。
(4) 根据模型对测试集进行测试,得到分类率。
(5) 计算k次求得的分类率的平均值,作为模型的最终分类率。
以五折交叉验证为例;
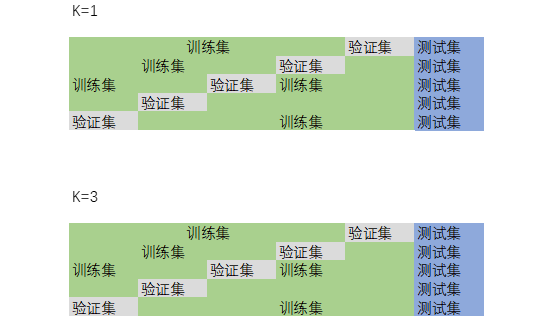
分别得出K=1时的平均分类准确度、K=1时的平均分类准确度……选出最优K值
距离度量
在KNN算法中,常用的距离有三种,分别为曼哈顿距离、欧式距离和闵可夫斯基距离。
距离通式:
当p=1时,称为曼哈顿距离
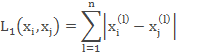
当p=2时,称为欧式距离
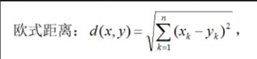
当p=∞时,
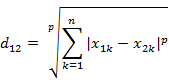
分类决策规则
:
1.多数表决:少数服从多数,即训练集里和预测的样本特征最近的K个样本,预测为里面有最多类别数的类别
2.加权表决:根据各个邻居与测试对象距离的远近来分配相应的投票权重。最简单的就是取两者距离之间的倒数,距离越小,越相似,权重越大,将权重累加,最后选择累加值最高类别属性作为该待测样本点的类别,类似大众评审和专家评审。
这两种确简单直接,在样本量少,样本特征少的时候有效,只适合数据量小的情况。因为我们经常碰到样本的特征数有上千以上,样本量有几十万以上,如果我们这要去预测少量的测试集样本,算法的时间效率很成问题。因此,这个方法我们一般称之为蛮力实现。比较适合于少量样本的简单模型的时候用。一个是KD树实现,一个是球树实现。