LeedCode排序专题
堆排序
堆其实就是利用完全二叉树的结构来维护的一维数组。
参考链接:https://www.cnblogs.com/lanhaicode/p/10546257.html
大顶堆:每个结点的值都大于或等于其左右孩子结点的值
小顶堆:每个结点的值都小于或等于其左右孩子结点的值
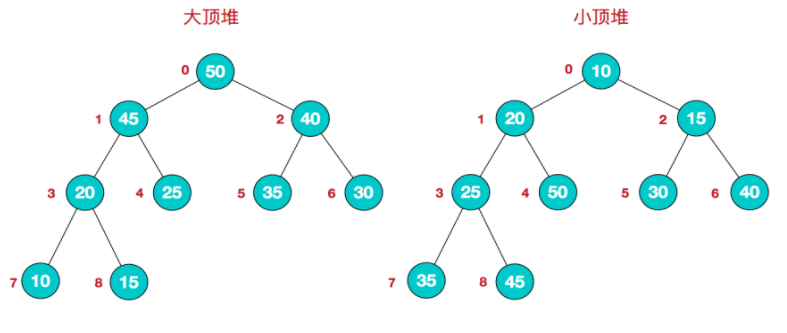
这里以上面左边的图为例子
先要找到最后一个非叶子节点,数组的长度为9,那么最后一个非叶子节点就是:长度/2-1,也就是9/2-1=3(就是20这个值),然后下一步就是比较该节点值和它的子树值,如果该节点小于其左右子树的值就交换(意思就是将最大的值放到该节点)
(图片来源:https://www.cnblogs.com/chengxiao/p/6129630.html)

(图片来源:https://www.cnblogs.com/chengxiao/p/6129630.html)
大顶堆:arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]
小顶堆:arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]
注意:Python 中没有大顶堆,只能将值取负保存在小顶堆来模拟。
适合类型的堆来进行排序
升序----使用大顶堆
降序----使用小顶堆
大顶堆排序的代码:
1 #include <stdio.h> 2 3 void Swap(int *heap, int len); /* 交换根节点和数组末尾元素的值 */ 4 void BuildMaxHeap(int *heap, int len);/* 构建大顶堆 */ 5 6 int main() 7 { 8 int a[6] = {7, 3, 8, 5, 1, 2}; 9 int len = 6; /* 数组长度 */ 10 int i; 11 12 for (i = len; i > 0; i--) 13 { 14 BuildMaxHeap(a, i); 15 Swap(a, i); 16 } 17 for (i = 0; i < len; i++) 18 { 19 printf("%d ", a[i]); 20 } 21 22 return 0; 23 } 24 /* Function: 构建大顶堆 */ 25 void BuildMaxHeap(int *heap, int len) 26 { 27 int i; 28 int temp; 29 30 for (i = len/2-1; i >= 0; i--) 31 { 32 if ((2*i+1) < len && heap[i] < heap[2*i+1]) /* 根节点大于左子树 */ 33 { 34 temp = heap[i]; 35 heap[i] = heap[2*i+1]; 36 heap[2*i+1] = temp; 37 /* 检查交换后的左子树是否满足大顶堆性质 如果不满足 则重新调整子树结构 */ 38 if ((2*(2*i+1)+1 < len && heap[2*i+1] < heap[2*(2*i+1)+1]) || (2*(2*i+1)+2 < len && heap[2*i+1] < heap[2*(2*i+1)+2])) 39 { 40 BuildMaxHeap(heap, len); 41 } 42 } 43 if ((2*i+2) < len && heap[i] < heap[2*i+2]) /* 根节点大于右子树 */ 44 { 45 temp = heap[i]; 46 heap[i] = heap[2*i+2]; 47 heap[2*i+2] = temp; 48 /* 检查交换后的右子树是否满足大顶堆性质 如果不满足 则重新调整子树结构 */ 49 if ((2*(2*i+2)+1 < len && heap[2*i+2] < heap[2*(2*i+2)+1]) || (2*(2*i+2)+2 < len && heap[2*i+2] < heap[2*(2*i+2)+2])) 50 { 51 BuildMaxHeap(heap, len); 52 } 53 } 54 } 55 } 56 57 /* Function: 交换交换根节点和数组末尾元素的值*/ 58 void Swap(int *heap, int len) 59 { 60 int temp; 61 62 temp = heap[0]; 63 heap[0] = heap[len-1]; 64 heap[len-1] = temp; 65 }
参考链接:https://www.cnblogs.com/lanhaicode/p/10546257.html