机器学习十讲第二讲

回归

基本数学知识—矩阵

• 矩阵可逆概念：对于n阶矩阵A，如果有一个n阶矩阵B，使得 AB = BA = E，则说矩阵 A 是可逆的，并把矩阵B称为矩阵A的逆矩阵
• 注意：若矩阵A可逆，则A的逆矩阵唯一
• 矩阵可逆的条件
  1. 行列式不等于0
  2. 矩阵满秩
  3. 行或列向量组线性无关

认识回归

回归最早由英国生物统计学家高尔顿和他的学生皮尔逊在研究父母亲和子女的身高遗传特性时提出，如今指用一个或多个自变量来预测因变量的数学方法。在机器学习中，回归指的是一类预测变量为连续值的有监督学习方法。

• 自变量：解释因变量变化的变量(X)
• 因变量：需要预测的变量(Y)

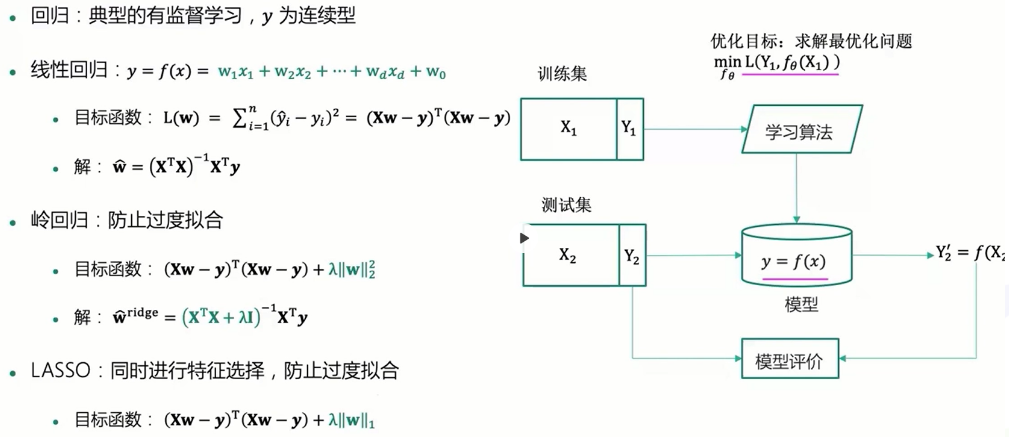
回归三大模型

线性回归

线性回归分类

• 一元线性回归

  模型：y=w1*x+w0，其中w0，w1为回归系数

  训练集：D={(x1,y1),…,(xn,yn)}

  优化目标：最小均方误差，找到一条直线y=w1*x+w0使得所有样本尽可能落在它的附近

• 多元线性回归

  模型： y是多个特征的线性组合，y=w1x1+w2x2+…+wd*xd+w0

  训练集：D={(x1,y1),…,(xn,yn)}

  优化目标：最小均方误差，寻找一个超平面，使得训练集中样本到超平面的误差平方和最小

线性回归问题

1、实际数据可能不是线性的

• 解决办法： 多项式回归，使用原始特征的二次项，三次项。问题在于会发生维度灾难，过度拟合

2、 多重共线性 ，如果变量之间存在较强的共线性，则矩阵 X^TX会近似奇异，导致参数估计不准确，造成过拟合

• 解决办法：在发生共线性的数据中仅选择一个，或者使用正则化，主成分回归，偏最小二乘回归

3、 过度拟合问题：当模型变量过多时，线性回归可能会出现过度拟合问题

• 解决办法：正则化，添加正则项或惩罚函数

为了解决自变量之间存在多重共线性或者自变量个数多于样本量的情况 ，提出了岭回归和LASSO回归

岭回归

• 岭回归分析（Ridge Regression）是一种改良的最小二乘法，其通过放弃最小二乘法的无偏性，以损失部分信息为代价来寻找效果稍差但回归系数更符合实际情况的模型方程。

• 简单来说，当方程变量中存在共线性时，一个变量的变化也会导致其他变量改变。岭回归就是在原方程的基础上加入了一个会产生偏差，但可以保证回归系数稳定的正常数矩阵KI。虽然会导致信息丢失，但可以换来回归模型的合理估计

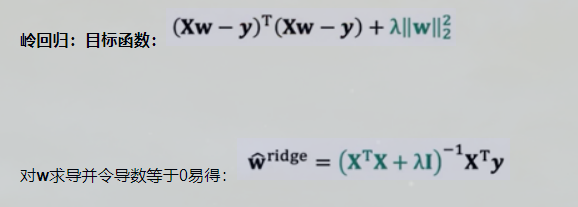
岭迹：当不断增大正则化参数λ，估计参数（岭回归系数）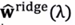

在坐标系上的变化曲线称为岭迹。岭迹波动很大，说明该变量有共线性。可根据岭迹做超参数λ的选择。

LASSO回归

• 一种系数压缩估计方法，基本思想是通过追求稀疏性自动选择重要的变量。

• 目标函数：

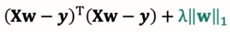
• 注：LASSO的解没有表达式，常用的求解算法包括坐标下降法，LARS算法，ISTA算法等

小结

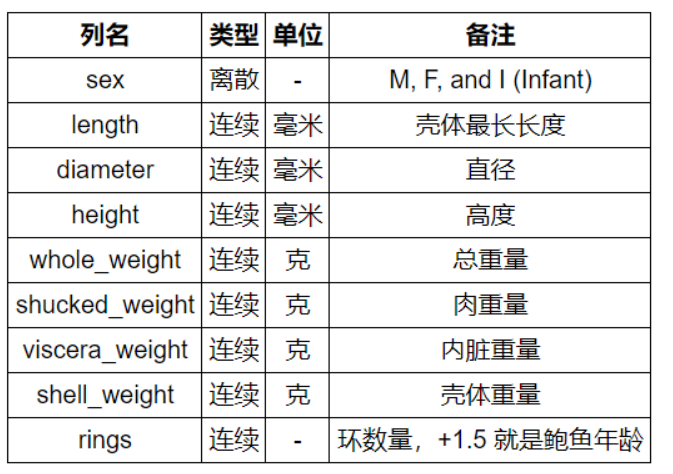
预测鲍鱼年龄案例

数据处理

#首先将数据集引入
import pandas as pd
import warnings
warnings.filterwarnings('ignore')
data = pd.read_csv("./input/abalone_dataset.csv")
#输出前五行
data.head()

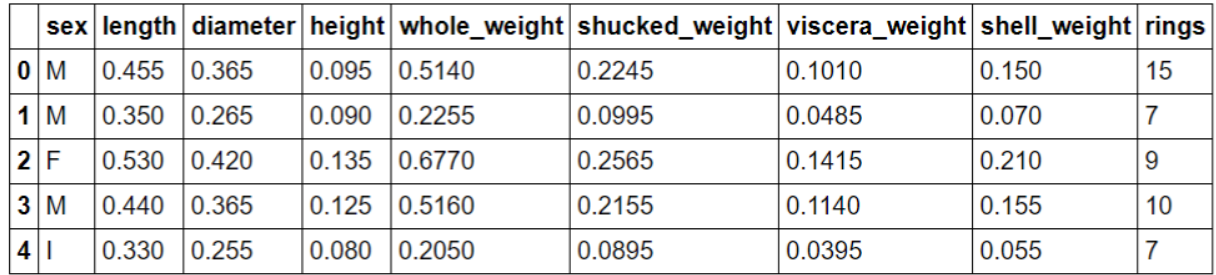
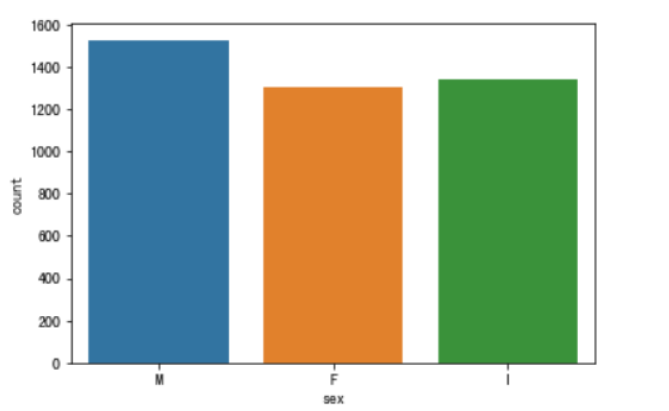
#使用seaborn绘制sex的取值分布条形图
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
sns.countplot(x = "sex", data = data)

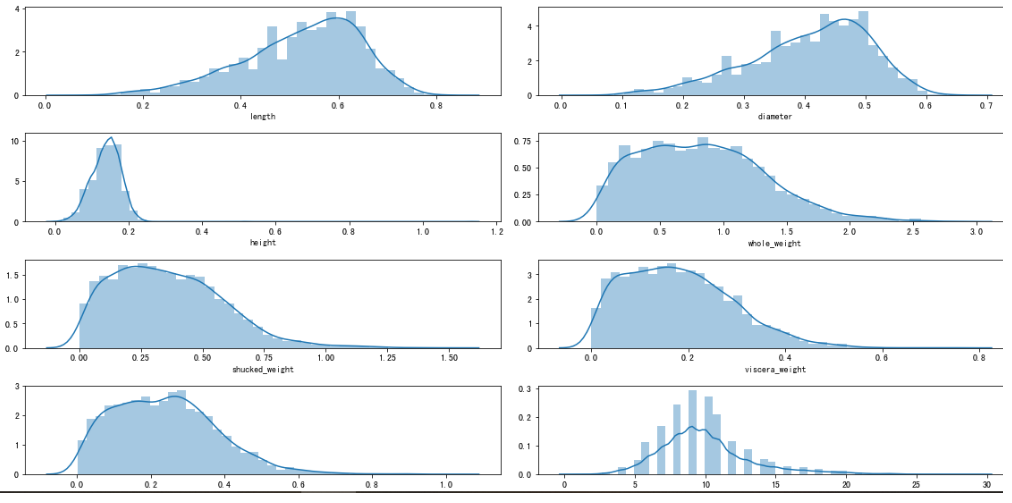
#绘制直方图观察特征取值
i = 1 # 子图记数
plt.figure(figsize=(16, 8))
for col in data.columns[1:]:
    plt.subplot(4,2,i)
    i = i + 1
    sns.distplot(data[col])  
plt.tight_layout()

#根据sex画出不同特征之间的点缀图，seaborn提供了pairplot方法
sns.pairplot(data,hue="sex")

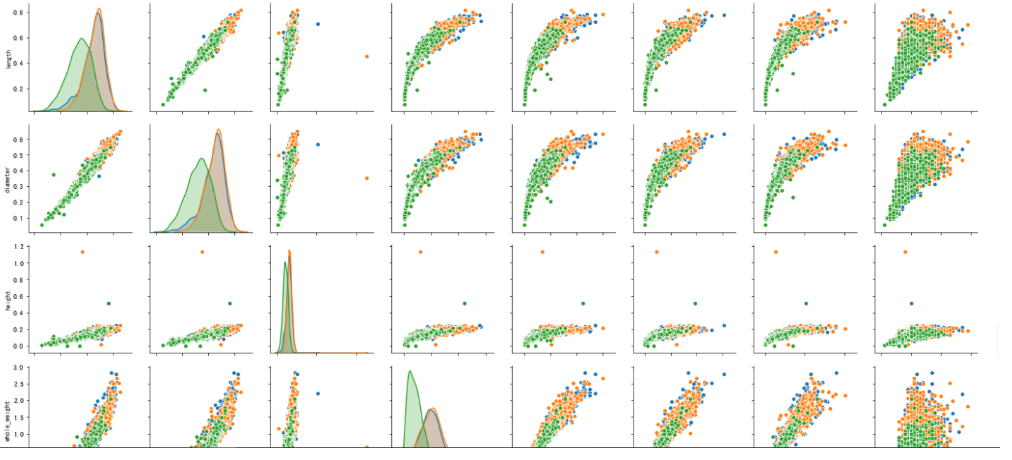
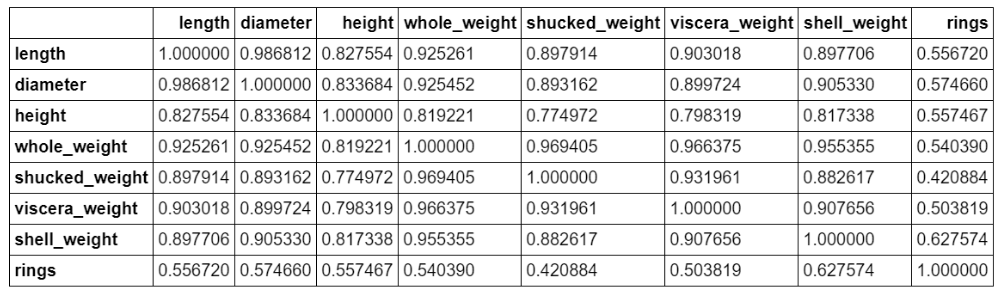
#计算特征之间的相关性
corr_df = data.corr()
corr_df
#为了能够直观看出关系，可以绘制热力图
fig, ax = plt.subplots(figsize=(12, 12))
#原图是绿色的，这里改成蓝色
ax=sns.heatmap(corr_df,linewidths=.5,cmap="Greens",annot=True,xticklabels=corr_df.columns, yticklabels=corr_df.index)
ax.xaxis.set_label_position('top') 
ax.xaxis.tick_top()

#OneHot编码处理
sex_onehot = pd.get_dummies(data["sex"], prefix="sex")
#参数sex_onehot.columns
data[sex_onehot.columns] = sex_onehot
#data.head(2)
#添加取值为1的特征列
data["ones"] = 1
#data.head(5)
#令age=rings+1.5
data["age"] = data["rings"] + 1.5
data.head(5)

#构造特征集
y = data["age"]
features_with_ones = ["length","diameter","height","whole_weight","shucked_weight","viscera_weight","shell_weight","sex_F","sex_M","ones"]
features_without_ones=["length","diameter","height","whole_weight","shucked_weight","viscera_weight","shell_weight","sex_F","sex_M"]
X = data[features_with_ones]

#训练集与测试集切分train_test_split
from sklearn import model_selection
X_train,X_test,y_train,y_test = model_selection.train_test_split(X,y,test_size=0.2, random_state=111)

使用线性回归预测

#使用之前介绍的sklearn作系数比对
from sklearn import linear_model
lr = linear_model.LinearRegression()
#刚才处理的时候将新设置的ones放了进去，而这里使用时不能添加ones列
lr.fit(X_train[features_without_ones],y_train)
w_lr = []
w_lr.extend(lr.coef_)
w_lr.append(lr.intercept_)
w1["lr_sklearn_w"] = w_lr
w1.round(decimals=2)

使用岭回归预测

def ridge_regression(X,y,ridge_lambda):
    #eye方法：生成单位矩阵
    penality_matrix = np.eye(X.shape[1])
    #令单位矩阵的最后一个元素=0
    penality_matrix[X.shape[1] - 1][X.shape[1] - 1] = 0
    #输入参数
    w = np.linalg.inv(X.T.dot(X) + ridge_lambda*penality_matrix).dot(X.T).dot(y)
    return w

#使用岭回归模型，与之前两个模型进行比对
w2 = ridge_regression(X_train,y_train,1.0)
w1["numpy_ridge_w"] = w2
w1.round(decimals=2)

#再与sklearn中的岭回归进行对比
from sklearn.linear_model import Ridge
ridge = linear_model.Ridge(alpha=1.0)
#这里还是使用无ones列的数据集
ridge.fit(X_train[features_without_ones],y_train)
w_ridge = []
w_ridge.extend(ridge.coef_)
w_ridge.append(ridge.intercept_)
w1["ridge_sklearn_w"] = w_ridge
w1.round(decimals=2)

使用LASSO预测

#使用LASSO
from sklearn.linear_model import Lasso
#alpha设置要小一些，否则
lasso = linear_model.Lasso(alpha=1)
lasso.fit(X_train[features_without_ones],y_train)
print(lasso.coef_)
print(lasso.intercept_)

三种模型评估

#平均绝对误差MAE
##使用sklearn.metrics进行预测
from sklearn.metrics import mean_absolute_error
#线性回归
y_test_pred_lr = lr.predict(X_test.iloc[:,:-1])
print(round(mean_absolute_error(y_test,y_test_pred_lr),4))

#岭回归
y_test_pred_ridge = ridge.predict(X_test[features_without_ones])
print(round(mean_absolute_error(y_test,y_test_pred_ridge),4))

#LASSO
y_test_pred_lasso = lasso.predict(X_test[features_without_ones])
print(round(mean_absolute_error(y_test,y_test_pred_lasso),4))

#决定系数R2
from sklearn.metrics import r2_score
#线性回归
print(round(r2_score(y_test,y_test_pred_lr),4))
#岭回归
print(round(r2_score(y_test,y_test_pred_ridge),4))
#LASSO
print(round(r2_score(y_test,y_test_pred_lasso),4))