树状数组BIT
现多用于计算前缀和,区间和,可在O(logN)时间内得到任意前缀和 。并且支持在O(logN)时间内动态单点修改
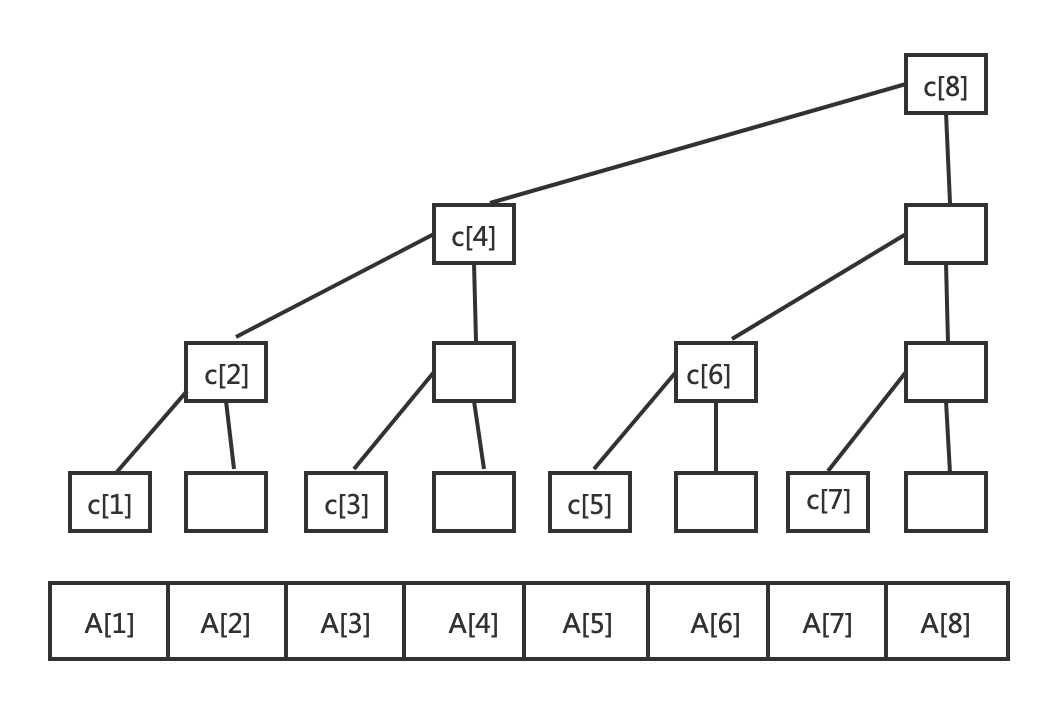
C1=A1
C2=A1+A2
C3=A3
C4=A1+A2+A3+A4
C5=A5
C6=A5+A6
C7=A7
C8=A1+A2+A3+A4+A5+A6+A7+A8
其中 C[i] = A[i - 2k+1] + A[i - 2k+2] + ... + A[i]; //k为i的二进制中从最低位到高位连续零的长度
例如i = 8(1000)时候,k = 3,可自行验证。
应用
针对一个数组A,有A0到An个元素,经过W次修改,每次修改一个元素的值,如何快速求其中任意区间内的和问题?
如何求和?
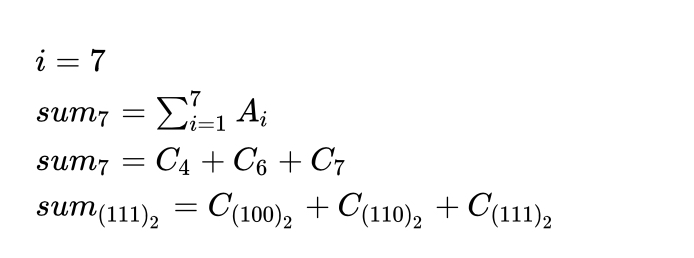
以7为例,sum求和0-7的计算方法,C的下标数值如何确定,即7开始不断的取lowbit(具体实现见代码lbt)
实现
package main
import "fmt"
type Bit struct {
BitTree []int
}
// 该函数也可写成 x&(-x)
//函数意义:求x中从最低位开始剔除一个1的数值,例如6(110),剔除最低位1转为4(100)需要减2(10),即lbt(6)=2
func (b *Bit) lbt(x int) int {
return x - (x & (x - 1))
}
func (b *Bit) Update(x int, v int) {
for i := x+1; i < len(b.BitTree); i += b.lbt(i) {
b.BitTree[i] += v
}
}
func (b *Bit) GetSum(x int) int {
sum := 0
for i := x+1; i > 0; i -= b.lbt(i) {
sum += b.BitTree[i]
}
return sum
}
func Init(a []int) Bit {
b := Bit{BitTree: make([]int, len(a)+1)}
for i := 0; i < len(a); i++ {
b.Update(i, a[i])
}
return b
}
func main(){
a := []int{1,1,1,1}
b := Init(a)
fmt.Println(b)
}