In this chapter, we discuss the support vector machine (SVM), an approach
for classification that was developed in the computer science community in
the 1990s and that has grown in popularity since then.
9.1Maximal Margin Classifier
What Is a Hyperplane(超平面)?
In a p-dimensional space, a hyperplane is a flat affine subspace of hyperplane dimension p − 1.
例如二维空间的超平面是一条线，三维空间的超平面是一个面。
In p-dimensional, a hyperplane is defined by the equation:
again in the sense that if a point X =(X1,X2, . . . , Xp)T in p-dimensional space (i.e. a vector of length p) satisfies
(9.2), then X lies on the hyperplane.
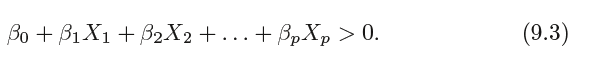
Then this tells us that X lies to one side of the hyperplane.
then X lies on the other side of the hyperplane.
9.1.2 Classification Using a Separating Hyperplane
Now suppose that we have a n×p data matrix X that consists of n training observations in p-dimensional space,
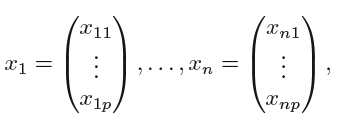
and that these observations fall into two classes—that is, y1, . . . , yn ∈{−1, 1} where −1 represents one class and 1 the other class.
Then a separating hyperplane has the property that
9.1.3 The Maximal Margin Classifier
That is, we can compute the (perpendicular垂直) distance from each training observation to a given separating hyperplane;
the smallest such distance is the minimal distance from the observations to the hyperplane, and is known as the margin（间隙）.
The maximal margin hyperplane is the separating hyperplane for which the margin is largest—that is, it is the hyperplane that has the farthest minimum distance
to the training observations.
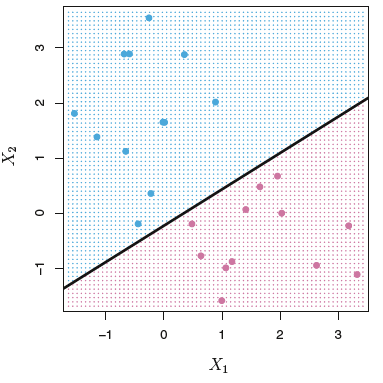
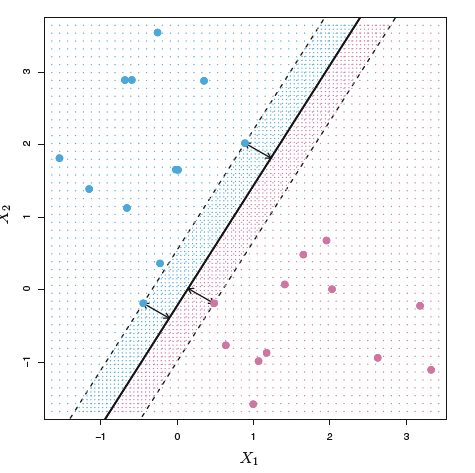
左图和右图是相同的数据集，右图是最大间隙超平面。右图中三个在虚线上的观测叫做支持向量（Support vector）,它们决定了最大间隙超平面的位置。
9.1.4 Construction of the Maximal Margin Classifier
the maximal margin hyperplane is the solution to the optimization(优化) problem：
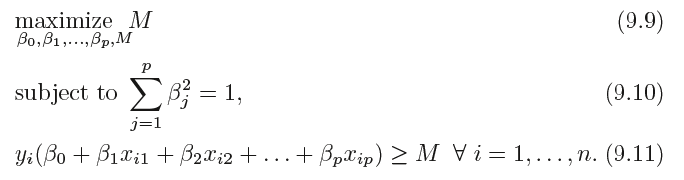
M represents the margin of our hyperplane
9.1.5 The Non-separable Case
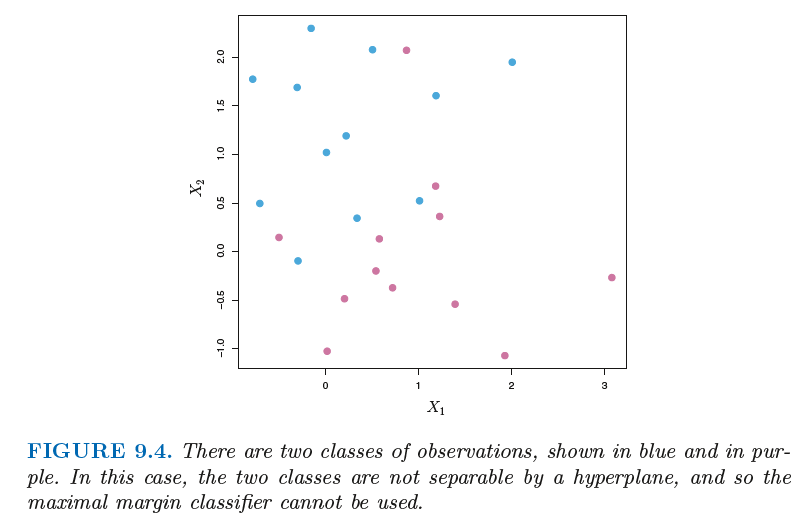
The generalization of the maximal margin classifier to the non-separable case is known as the support vector classifier.
9.2 Support Vector Classifiers
9.2.1 Overview of the Support Vector Classifier
The support vector classifier, sometimes called a soft margin classifier.
Rather than seeking the largest possible margin so that every observation is not only on the correct side of the hyperplane but also on the correct side of the margin,
we instead allow some observations to be on the incorrect side of the margin, or even the incorrect side of the hyperplane.
- Greater robustness to individual observations, and
- Better classification of most of the training observations
9.2.2 Details of the Support Vector Classifier
支持向量分类能保证大部分的观测值分类正确，但仍会有一些误分类。
It is the solution to the optimization problem：
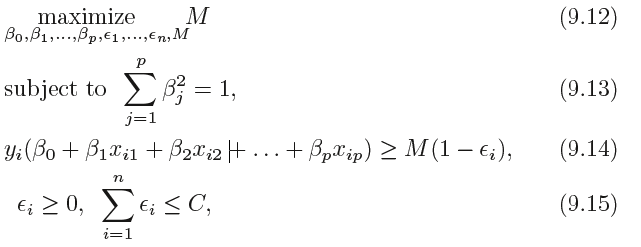
其中， C 是非负的调节参数。跟式(9. 11 )中一样， M 是间隔的宽度，目标是最大化M。在
(9. 14) 中，
是松弛变量(slack variahle) ，松弛变量的作用是允许训练观测中有
小部分观测可以落在间隔的错误的一侧或是超平面的错误的一侧。
If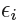 
> 0 then the ith observation is on the wrong side of the margin, and we say that the ith observation has violated the margin.
> 1 then it is on the wrong side of the hyperplane.
C bounds the sum of the ’s, and so it determines the number and severity of the violations
to the margin (and to the hyperplane) that we will tolerate.
When C is small，have low bias but high variance.
When C is larger, the margin is wider and more biased but may have lower variance.
9.3 Support Vector Machines
9.3.1 Classification with Non-linear Decision Boundaries
在支持向量分离器中可以使用预测变量的二次多项式、三次多项式甚至更高阶来扩大特征空间。也可以使用预测变量的其他函数来扩大特征空间。
9.3.2 The Support Vector Machine
The support vector machine (SVM) is an extension of the support vector machine classifier that results from enlarging the feature space in a specific way,
using kernels.
The main idea is that we may want to enlarge our feature space in order to accommodate a non-linear boundary between the classes.
The linear support vector classifier can be represented as：
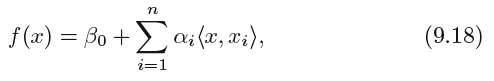
where there are n parameters αi, i = 1, . . . , n, one per training observation.
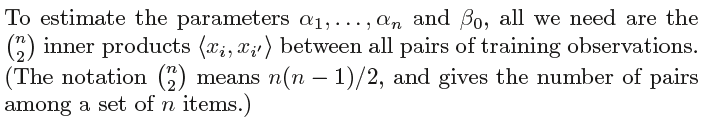
This is known as a polynomial kernel of degree d, where d is a positive polynomial integer.
Note that in this case the (non-linear) function has the form
When d = 1, then the SVM reduces to the support vector classifier seen earlier in this chapter.
Another popular choice is the radial kernel(径向核函数), which takes the form
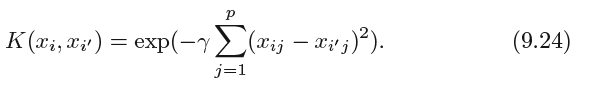
9.4 多分类的SVM
One-Versus-One Classification
One-Versus-All Classification
