1 枚举类型


在Java中,枚举类型本质上其实就是一个类,枚举中的常量都是该枚举类型的实例。枚举类型是引用类型!枚举不属于原始数据类型,它的每个具体值都引用一个特定的对象。相同的值则引用同一个对象。可以使用“==”和equals()方法直接比对枚举变量的值,换句话说,对于枚举类型的变量,“==”和equals()方法执行的结果是等价的。
2 反码、补码原码
原码就是二进制定点表示法,即最高位为符号位,“0”表示正,“1”表示负,其余位表示数值的大小。
反码:正数的反码与其原码相同;负数的反码是对其原码逐位取反,但符号位外。
补码:正数的补码与其原码相同;负数的补码是在其反码的末位加1
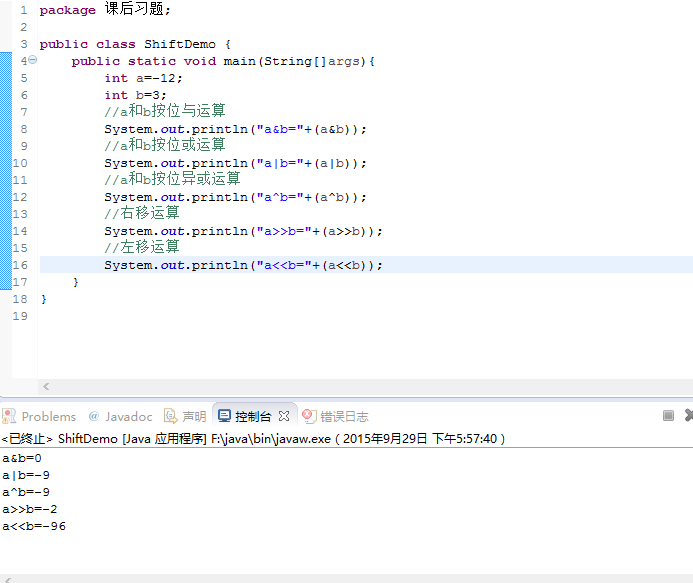

数值在计算机中表示形式为机器数,计算机只能识别0和1,使用的是二进制,而在日常生活中人们使用的是十进制.数值有正负之分,计算机就用一个数的最高位存放符号(0为正,1为负).这就是机器数的原码了.假设机器能处理的位数为8.即字长为1byte,原码能表示数值的范围为 (-127~-0 +0~127)共256个. 有了数值的表示方法就可以对数进行算术运算.但是很快就发现用带符号位的原码进行乘除运算时结果正确,而在加减运算的时候就出现了问题,如下:
假设字长为8bits
( 1 ) 10- ( 1 )10 = ( 1 )10 + ( -1 )10 = ( 0 )10 (00000001)原 + (10000001)原 = (10000010)原 = ( -2 )
显然不正确. 因为在两个整数的加法运算中是没有问题的,于是就发现问题出现在带符号位的负数身上,对除符号位外的其余各位逐位取反就产生了反码.反码的取值空间和原码相同且一一对应. 下面是反码的减法运算:
( 1 )10 - ( 1 ) 10= ( 1 ) 10+ ( -1 ) 10= ( 0 )10 (00000001) 反+ (11111110)反 = (11111111)反 = ( -0 )
有问题.
( 1 )10 - ( 2)10 = ( 1 )10 + ( -2 )10 = ( -1 )10 (00000001) 反+ (11111101)反 = (11111110)反 = ( -1 )
正确
问题出现在(+0)和(-0)上,在人们的计算概念中零是没有正负之分的.(印度人首先将零作为标记并放入运算之中,包含有零号的印度数学和十进制计数对人类文明的贡献极大). 于是就引入了补码概念. 负数的补码就是对反码加一,而正数不变,正数的原码反码补码是一样的.在补码中用(-128)代替了(-0),所以补码的表示范围为: (-128~0~127)共256个.
注意:(-128)没有相对应的原码和反码, (-128) = (10000000) 补码的加减运算如下:
( 1 ) 10- ( 1 ) 10= ( 1 )10 + ( -1 )10 = ( 0 )10 (00000001)补 + (11111111)补 = (00000000)补 = ( 0 )
正确
( 1 ) 10- ( 2) 10= ( 1 )10 + ( -2 )10 = ( -1 )10 (00000001) 补+ (11111110) 补= (11111111)补 = ( -1 )
正确
所以补码的设计目的是: ⑴使符号位能与有效值部分一起参加运算,从而简化运算规则. ⑵使减法运算转换为加法运算,进一步简化计算机中运算器的线路设计
3 变量的作用域
每个变量都有一个“有效”的区域(称为“作用域”),出了这个区域,变量将不再有效。Java变量遵循“同名变量的屏蔽原则”

4 在运行时读取用户输入
(1)方法一:使用JOptionPane类的showInputDialog方法。
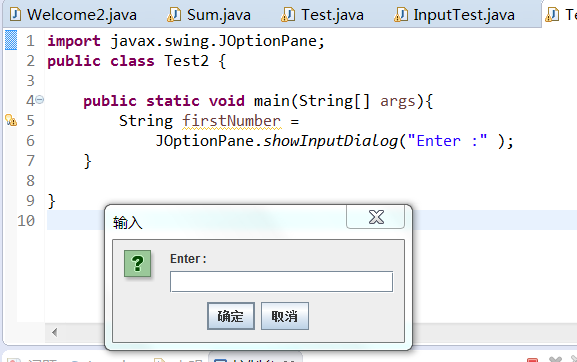
(2)方法二:使用Scanner类(JDK5.0以上)

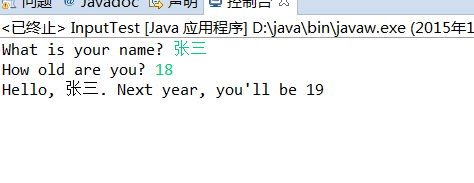
5 Java中的类型转换


使用double类型的数值进行计算, 其结果是不精确的。
为什么double类型的数值进行运算得不到“数学上精确”的结果?
事实上浮点运算很少是精确的,只要是超过精度能表示的范围就会产生误差。往往产生误差不是 因为数的大小,而是因为数的精度。因此,产生的结果接近但不等于想要的结果。尤其在使用 float 和 double 作精确运算的时候要特别小心。
可以考虑采用一些替代方案来实现。如通过 String 结合 BigDecimal 或 者通过使用 long 类型来转换。还可以用使用BigDecimal类来实现。(注意:在构建BigDecimal对象时应使用字符串而不是double数值)


6 字串联接操作

