Enhancing VAEs for Collaborative Filtering: Flexible Priors & Gating Mechanisms

论文：《Enhancing VAEs for Collaborative Filtering: Flexible Priors & Gating Mechanisms》，RecSys2019

代码：https://github.com/psywaves/EVCF

一、概述

目前出现了很多将深度学习与推荐系统相结合的研究工作，这篇论文也是这个思路。它重点关注如何基于自编码器和生成模型建模用户偏好隐变量，主要创新就是将其他领域的一些现有方法应用到了推荐系统。这类方法的思路是将每个用户的偏好编码为一个隐变量，需要推荐的时候，就根据这个隐变量重构该用户和产品的交互历史，也就是用户消费每个产品的概率。目前在这类研究中，变分自编码器和协同过滤结合的方法取得了最好的效果。

然而，当前模型还存在两个问题，这也就是本文的动机：

1. VAEs使用的先验分布对于协同过滤来说可能过于严格，阻碍了模型学习用户偏好隐变量。
2. 用户-产品交互历史具有其自身的特征，可以探索更有效的模型结构来学习更深层次的用户偏好隐变量。

因此，该论文提出了一个基于VampPrior (Tomczak, J. M., & Welling, M., 2017)的层次变分自编码器，从用户交互历史中学习用户偏好更加丰富的表示。此外，该论文还使用了门控机制(GLUs)用于控制信息在网络中的流动。论文最终在MovieLens-20M和Netflix两个数据集上进行了实验，发现与矩阵分解和自编码器方法相比在NDCG和召回率方面有较大提升。

创新点总结如下：

1. 第一个指出了VAE-CF框架下先验分布过于严格问题，并且表明了放宽分布可以获得更好的推荐效果。
2. 表明了引入门控机制对于AE-CF框架在学习更深，更复杂的交互历史表示中非常有帮助。
3. 提出的模型在协同过滤任务中获得了最好的效果。

二、背景

该论文是在Multi-VAE (Liang, Dawen, et al., 2018)的基础上进行扩展的，Multi-View首次将变分自编码器和协同过滤结合在了一起。

1 问题定义

假设(u in {1,dots,N})表示用户，(i in {1,dots,M})表示产品，二元数据集(X={x_1,dots,x_N})表示每个用户(u)的交互历史，其中(x_u in mathbb{I}^M)有(M)维。要学习的就是用户(u)的偏好隐变量(z_u in mathbb{R}^D)。

2 VAE-CF方法

Multi-VAE模型的生成过程描述如下：对于每个用户(u)，首先从标准正态先验分布中采样隐变量(z_u)，然后通过生成网络重构用户和产品的交互历史(x_u)，也就是产生一个多项分布：

[egin{aligned} z_u sim N(0, mathbf{I}_D), quad pi(z_u) propto exp[f_{ heta}(z_u)] \ x_u sim Multi(N_u, pi(z_u)) end{aligned} ]

接下来就是和标准的VAE一样了，通过ELBO进行优化：

[egin{aligned} log p(x_u; heta) &geq mathbb{E}_{q_{phi}(z_u|x_u)}[log p_{ heta}(x_u|z_u)] \ & -KLleft( q_{phi}(z_u|x_u)||p(z_u) ight) \ &equiv mathcal{L}(x_u; heta,phi) end{aligned} ]

其中(q_{phi}(z|x))和(p_{ heta}(x|z))分别是编码器和解码器。

变分自编码器的基础知识请移步这里。

三、方法

变分自编码器在图片生成等领域研究广泛，其中有研究指出其先验分布过于严格，可能限制了模型性能。但是，这个问题在推荐系统领域还没有人指出。

1 灵活先验分布

和其他工作一样，ELBO优化项可以重写为下列形式：

[egin{aligned} mathcal{L}(x_u; heta,phi) &= mathbb{E}_{x sim q_(x)}left[mathbb{E}_{q_{phi}(z|x)}[log p_{ heta}(x|z)] ight] \ &+mathbb{E}_{x sim q_(x)}left[mathbb{H}[q_{phi}(z|x)] ight] \ &-mathbb{E}_{z sim q_(z)}left[-log p_{lambda}(z) ight] end{aligned} ]

其中，第一项是重构损失，第二项是变分后验分布期望熵，第三项是聚合后验分布(q(z)=frac{1}{N}sum_{u=1}^N q_{phi}(z|x_u))和先验分布的交叉熵。

虽然编码器尝试使后验分布匹配先验分布，但不能保证简单的单峰先验分布就很好了。由于对人类偏好进行建模是一个复杂的问题，因此论文认为在协同过滤的情况下可以放宽先验分布的限制。

2 VampPrior

VampPrior使用以(K)个可学习的伪输入为条件的变分后验的混合分布来近似最优先验：

[p_{lambda}(z)=frac{1}{K}sum_{k=1}^K q_{phi}(z|u_k) ]

其中(K ll N)是(M)维伪输入(u_k)的个数。伪输入是通过反向传播学习的，可以认为是先验的超参数。

3 层次随机单元

为了学习更丰富的隐表示，作者同样借鉴了VampPrior工作中的层次随机单元，这同样还没用于协同过滤。

原始的隐变量(z)被替换为具有层次结构的(z_1)和(z_2)。编码器部分修改为:

[q_{phi}(z_1|x,z_2)q_{varphi}(z_2|x) ]

解码器部分修改为

[p_{ heta}(x|z_1,z_2)p_{lambda}(z_1|z_2)p(z_2) ]

其中，(p(z_2))使用VampPriors定义为(p_(z_2)=frac{1}{K}sum_{k=1}^K q_{phi}(z_2|u_k))。其他的条件分布都是通过神经网络建模。

4 门控机制

随着神经网络的结构越来越深，非循环神经网络同样存在无法正确地将信息从底层传播到顶层的问题。因此论文借鉴了Gated CNN中的门控机制，用来训练更深的网络：

[h_l(X) = (X ast W + b) otimes sigma(X ast V + c) ]

其中(otimes)表示按元素乘积，(W,V,b,c)都是参数，(sigma)是sigmoid激活函数。作者认为这样能够增加网络的建模能力以允许更高级别的交互。

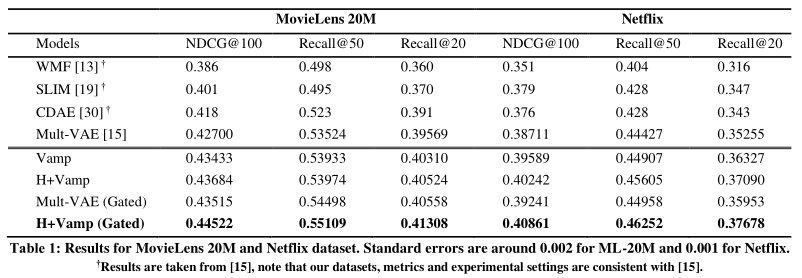
四、实验

该论文在MovieLens-20M和Netflix数据集上进行实验，评价指标采用了Recall@K和NDCG@K，都是排序相关的评测方法，下面是实验主要结果。