Memory-based Graph Networks

论文：《Memory-based Graph Networks》，ICLR2020

代码：https://github.com/amirkhas/GraphMemoryNet

概述

图神经网络(GNNs)是一类深度模型，可处理任意拓扑结构的数据。比如社交网络、知识图谱、分子结构等。GNNs通常被用来根据节点的交互关系学习节点的向量表示，典型的模型有gated GNN(Li et al., 2015)、MPNN(Giler et al., 2017)、GCN(Kipf & Welling, 2016)和GAT(Velikovi et al., 2018)。GNNs方法通常优于传统的随机游走、矩阵分解、核方法和概率图模型。

但是，这些模型无法学习到层次表示，因为它们没有利用图的组合性质。DiffPool (Ying et al., 2018)、TopKPool (Gao & Ji, 2019)、SAGPool (Lee et al., 2019)等模型引入参数化的图池化层，通过堆叠交错层和池化层来学习层次图表示。但这些模型的计算效率不高，因为它们需要在每个池化层后进行消息传递计算。

本论文介绍了一个能够同时进行图表示学习和节点聚类的记忆层，该记忆层由多组(multi-head)记忆键和卷积运算组成。记忆键被视为聚类中心，而卷积运算用来聚合多组结果。记忆层的输入叫做query，是前一层输出的节点表示，记忆层的输出是聚类后的节点表示。这种记忆层不显式依赖节点的连接信息，因此不存在过度平滑问题(Xu et al., 2018)，同时也改进了效率和性能。

作者在论文中提出了两种基于记忆层的网络，分别叫做memory-based GNN(MemGNN)和graph memory network(GMN)。其中MemGNN就是首先使用GNN学习节点的初始表示然后堆叠记忆层学习层次表示；GMN则不依赖GNN，因此也不需要消息传递的计算。

相关工作

方法

下面开始讲记忆层究竟是什么，以及由此而来的两种网络架构，即GMN和MemGNN。

记忆层

第(l)层的记忆层可以表示为(mathcal{M}^{(l)}:mathbb{R}^{n_l imes d_l} longmapsto mathbb{R}^{n_{l+1} imes d_{l+1}})，记忆层输入(n_l)个维度为(d_l)的查询向量，生成(n_{l+1})个维度为(d_{l+1})的查询向量(下个记忆层的查询向量)。因为要自底向上学习图层次表示，要保证(n_{l+1} lt n_l)。

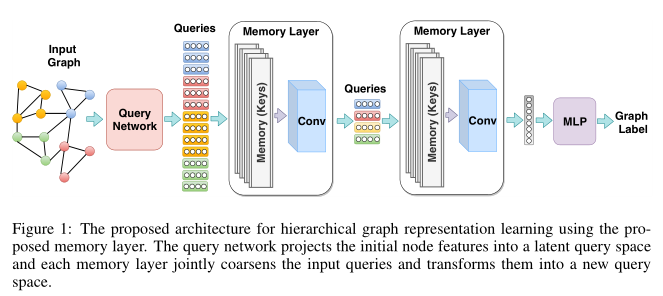
上图就是记忆层的示意图，假设其中有(|h|)组记忆键。现在来看看记忆层是怎么实现聚类的。首先，假设第(l)层记忆层的输入为(mathbf{Q}^{(l)} in mathbb{R}^{n_l imes d_l})，一组记忆键(mathbf{K}^{(l)} in mathbb{R}^{n_{l+1} imes d_l})可以看作是(mathbf{Q}^{(l)})的聚类中心。为了衡量(mathbf{Q}^{(l)})和(mathbf{K}^{(l)})每个分量之间的相似度，作者借鉴Xie et al., 2016的工作，使用t分布作为核函数。因此查询(q_i)和记忆键(k_j)的正则化的相似度定义为：

[C_{i,j}=frac{(1+||q_i-k_j||^2/ au)^{-frac{ au + 1}{2}}}{sum_{j^{'}}(1+||q_i-k_{j^{'}}||^2/ au)^{-frac{ au + 1}{2}}} ]

(C_{i,j})就是将节点(i)分配到类簇(j)的概率，或者说(q_i)和(k_j)之间的注意力权重。( au)是t分布的自由度。前面我们说到，记忆键总共有(|h|)组，因此实际上上述聚类要计算(|h|)次，得到结果为([mathbf{C}_0^{(l)} dots mathbf{C}_{|h|}^{(l)}] in mathbb{R}^{|h| imes n_{l+1} imes n_l})。为了将(h)组结果聚合为一组结果，作者将三个维度分别看作深度、高度和宽度，然后使用一个(1 imes 1)的卷积进行聚合：

[mathbf{C}^{(l)}= ext{softmax}(Gamma_{phi}(Vert_{k=0}^{|h|}mathbf{C}_k^{(l)})) in mathbb{R}^{n_l imes n_{l+1}} ]

其中，(Gamma_{phi})是(1 imes 1)的卷积，(mathbf{C}^{(l)})就是聚合后的分配矩阵。

之后，值(value)矩阵(mathbf{V}^{(l)} in mathbb{R}^{n_{l+1} imes d_l})由下式定义：

[mathbf{V}^{(l)} = mathbf{C}^{(l)T}mathbf{Q}^{(l)} in mathbb{R}^{n_{l+1} imes d_l} ]

由于(mathbf{V}^{(l)})元素维度和(mathbf{Q}^{(l)})元素维度相同，作者认为这就表示在相同空间对节点聚类，之后还要经过一个单层前向网络将(mathbf{V}^{(l)})投影为新的查询：

[mathbf{Q}^{(l+1)} = sigma(mathbf{V}^{(l)}mathbf{W}) in mathbb{R}^{n_{l+1} imes d_{l+1}} ]

其中(sigma)是LeankyReLU激活函数。(mathbf{Q}^{(l+1)})将作为下一个记忆层的查询。

对于图分类任务，我们可以通过堆叠记忆层最终获得整个图的向量表示，然后用全连接层进行分类：

[mathcal{Y}= ext{softmax}( ext{MLP}(mathcal{M}^{(l)}(mathcal{M}^{(l-1)}(dots mathcal{M}^{(0)}(mathbf{Q}^{(0)}))))) ]

其中，(mathbf{Q}^{(0)}=f_q(g))是将图(g)输入网络(f_g)得到的初始查询表示，也就是初始节点向量。根据(f_q)的不同，作者引出了两种模型，即GMN和MemGNN。

GMN架构

GMN将图中节点表示视为排列不变(permutation-invariant)集，也就是不考虑它们之间的空间关系，因此也不需要使用到图神经网络中的消息传递机制。但是，图中节点毕竟是存在拓扑关系的，完全不考虑是行不通的，因此作者考虑的是把节点的拓扑关系编码到节点的初始表示中。更具体地说，作者使用带重启的随机游走(RWR)(Pan et al., 2004)来计算拓扑嵌入，然后按行对它们进行排序，以强制节点嵌入保持顺序不变。得到包含拓扑信息的节点表示(mathbf{X} in mathbb{R}^{n imes d_{in}})后，初始的查询表示通过两层前向网络计算得到：

[egin{aligned} mathbf{Q}^{(0)} &=f_q(g) \ &=sigma([sigma(mathbf{SW}_0) Vert X]mathbf{W}_1) end{aligned} ]

其中(mathbf{W}_0 in mathbb{R}^{n imes d_{in}})和(mathbf{W}_1 in mathbb{R}^{2d_{in} imes d_{0}})是参数，(mathbf{S} in mathbb{R}^{n imes n})是图扩散矩阵，(Vert)表示拼接操作，(sigma)是LeakyReLU激活函数。

MemGNN架构

MemGNN直接使用图神经网络计算初始查询：

[egin{aligned} mathbf{Q}^{(0)} &=f_q(g) \ &=G_{ heta}(mathbf{A},mathbf{X}) end{aligned} ]

其中，(G_{ heta})是任意的图神经网络。作者在实现时使用了GAT模型的改进版e-GAT，也就是在计算注意力权重时考虑了边特征。注意力权重计算公式为：

[alpha_{ij}=frac{exp(sigma(mathbf{W}[mathbf{W}_n h_i^{(l)} Vert mathbf{W}_n h_j^{(l)} Vert mathbf{W}_e h_{i ightarrow j}^{(l)}]))}{sum_{k in mathcal{N}_i}exp(sigma(mathbf{W}[mathbf{W}_n h_i^{(l)} Vert mathbf{W}_n h_k^{(l)} Vert mathbf{W}_e h_{i ightarrow k}^{(l)}]))} ]

其中(h_i^{(l)}, h_{i ightarrow j}^{(l)})分别是节点表示和边表示，(mathbf{W}_n, mathbf{W}_e)分别是节点权重和边权重，(mathbf{W})是前向网络参数，(sigma)是LeakyReLU激活函数。

模型训练

模型的损失包含两部分，有监督损失和无监督损失。有监督损失(mathcal{L}_{sup})来自图分类或者图回归损失。无监督损失用于鼓励模型学习利于聚类的表示，由(mathbf{C}^{(l)})和辅助分布(mathbf{P}^{(l)})之间的KL散度定义：

[egin{aligned} mathcal{L}_{KL}^{(l)} &= KL(mathbf{P}^{(l)}||mathbf{C}^{(l)}) \ &=sum_i sum_j P_{ij}^{(l)} log frac{P_{ij}^{(l)}}{C_{ij}^{(l)}} end{aligned} ]

其中辅助分布(mathbf{P}^{(l)})的计算和Xie et al., 2016一样，

[P_{ij}^{(l)} = frac{(C_{ij}^{(l)})^2 / sum_i C_{ij}^{(l)}}{sum_{j^{'}}(C_{ij^{'}}^{(l)})^2 / sum_i C_{ij^{'}}^{(l)}} ]

因此模型最终的损失定义为

[mathbf{L} = frac{1}{N}sum_{n=1}^Nleft(lambda mathcal{L}_{sup} + (1-lambda)sum_{l=1}^L mathcal{L}_{KL}^{(l)} ight) ]

为了使训练更稳定，(mathcal{L}_{sup})产生的的梯度每个batch进行反向传播，而(mathcal{L}_{KL}^{(l)})产生的梯度每个epoch反向传播一次，可以通过反复调整(lambda)的取值为0或1实现。这是因为快速地调整聚类中心，也就是记忆键，可能会导致训练不稳定。

实验

论文主要关注图分类和图回归任务，使用了5个图分类数据集和2个图回归数据集：

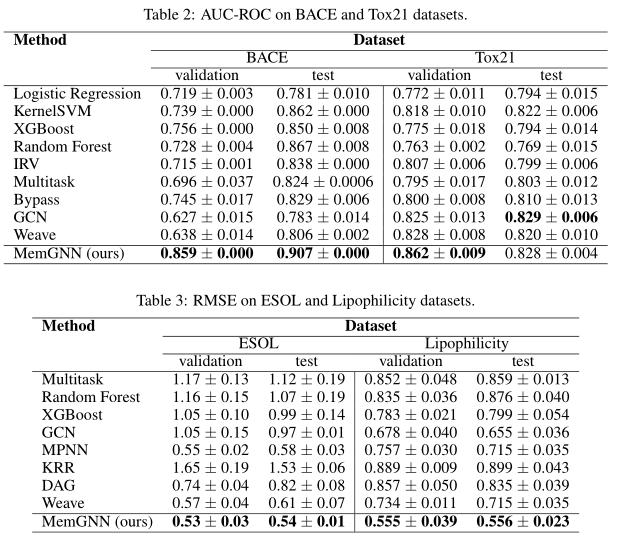
主要实验结果如下面几幅图所示：